题目内容
求证:
+
+…+
=
.
| 1 |
| 1×2×3 |
| 1 |
| 2×3×4 |
| 1 |
| n(n+1)(n+2) |
| n(n+3) |
| 4(n+1)(n+2) |
考点:分式的加减法
专题:证明题
分析:已知等式左边变形后,抵消合并,计算得到结果,与右边相等即可得证.
解答:证明:方程左边=
[
-
+
-
+…+
-
]=
[
-
]=
=
=右边,
则原式成立.
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
| 1 |
| (n+1)(n+2) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| (n+1)(n+2) |
| n2+3n+2-2 |
| 4(n+1)(n+2) |
| n(n+3) |
| 4(n+1)(n+2) |
则原式成立.
点评:此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图L1∥L2∥L3,AB=4,DE=3,EF=6,则BC的长( )
如图L1∥L2∥L3,AB=4,DE=3,EF=6,则BC的长( )| A、4 | B、6 | C、8 | D、10 |
下列各式计算正确的是( )
A、
| ||||||
B、-3
| ||||||
C、
| ||||||
D、
|
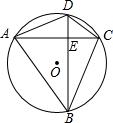 如图,四边形ABCD是⊙O的内接四边形,AC⊥BD于点E,若AB=8,CD=6,则⊙O的半径是多少?
如图,四边形ABCD是⊙O的内接四边形,AC⊥BD于点E,若AB=8,CD=6,则⊙O的半径是多少? △ABC在平面直角坐标系中的位置如图.
△ABC在平面直角坐标系中的位置如图.