题目内容
7．
一只蜘蛛正处于一个正方体的一个顶点A处，一只苍蝇处于此正方体的另一个顶点B处（如图所示），如果此正方体的棱长恰为10cm，试问蜘蛛想捉到苍蝇的最短路线是10$\sqrt{5}$cm．
分析 把此正方体的一面展开，然后在平面内根据两点之间，线段最短，即可得出最短的路径．
解答 
解：如图所示：AB即为最短路线，
则在Rt△ABC中，AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{2{0}^{2}+1{0}^{2}}$=10$\sqrt{5}$cm，
答：蜘蛛所走的最短路线长度是10$\sqrt{5}$cm．
点评 此题主要考查了平面展开图最短路径问题以及勾股定理，得出爬行路线是解题关键．
练习册系列答案
相关题目
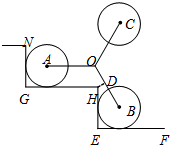如图是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图，定长的轮架杆OA，OB，OC抽象为线段，有OA=OB=OC，且∠AOB=120°，折线NG-GH-HE-EF表示楼梯，CH，EF是水平线，NG，HE是铅垂线，半径相等的小轮子⊙A，⊙B与楼梯两边相切，且AO∥GH．