Question

9．对于抛物线y=-x²+4x-3．

（1）它与x轴交点的坐标为（1，0）、（3，0），与y轴交点的坐标为（0，-3），顶点坐标为（2，1）；
（2）在坐标系中利用描点法画出此抛物线；

x	…	0	1	2	3	4	…
y	…	-3	0	1	0	-3	…

（3）结合图象回答问题：当1＜x＜4时，y的取值范围是-3＜y＜0．

Answer 1

分析 （1）令y=0得：-x²+4x-3=0，求得方程的解，从而得到抛物线与x轴交点的坐标，令x=0，求得y值，从而求得抛物线与y轴的交点坐标，根据二次函数图象的顶点式，可得顶点坐标；
（2）利用列表、描点、连线的方法画出图形即可；
（3）根据函数图象回答即可．

解答 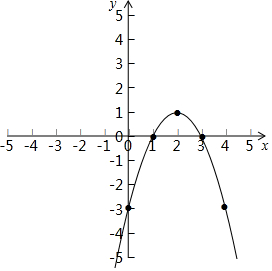解：（1）在y=-x²+4x-3中，令y=0，则-x²+4x-3=0，
解得：x₁=1，x₂=3，
∴抛物线y=-x²+4x-3与x轴交点的坐标为（1，0），（3，0）；
令x=0，则y=-3，
∴抛物线y=-x²+4x-3与y轴交点的坐标为（0，-3）；
∵y=-x²+4x-3=-（x-2）²+1，
∴顶点坐标为（2，1）；
故答案为：（1，0），（3，0），（0，-3），（2，1）；

（2）当x=0，1，2，3，4时，y=-3，0，1，0，-3；
如图所示，
故答案为：0，1，2，3，4，-3，0，1，0，-3；

（3）由图象知：当1＜x＜4时，y的取值范围是-3＜y＜0．
故答案为：-3＜y＜0．

点评 本题主要考查的是抛物线与x轴交点的坐标、画函数的图象，利用函数图象求得y的取值范围是解题的关键．