题目内容
13.阅读下列材料:如图1,在四边形ABCD中,已知∠ACB=∠BAD=105°,∠ABC=∠ADC=45°.求证:CD=AB.
小刚是这样思考的:由已知可得,∠DCA=60°,∠DAC=75°,∠CAB=30°,∠ACB+∠DAC=180°,由求证及特殊角度数可联想到构造特殊三角形.即过点A作AE⊥AB交BC的延长线于点E,则AB=AE,∠E=∠D.
∵在△ADC与△CEA中,
$\left\{\begin{array}{l}{∠D=∠E}\\{∠DAC=∠ECA=75°}\\{AC=CA}\end{array}\right.$∴△ADC≌△CEA,得CD=AE=AB.
请你参考小刚同学思考问题的方法,解决下面问题:
如图2,在四边形ABCD中,若∠ACB+∠CAD=180°,∠B=∠D,请问:CD与AB是否相等?若相等,请你给出证明;若不相等,请说明理由.
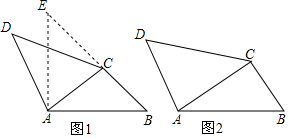
分析 结论:CD=AB.延长BC至E使AE=AB,则∠B=∠E.只要证明△CAD≌△ACE,得CD=AE,由此即可证明.
解答 解:结论:CD=AB.
证明:延长BC至E使AE=AB,则∠B=∠E.
∵∠B=∠D
∴∠D=∠E
∵∠ACB+∠CAD=180°,∠ACB+∠ACE=180°,
∴∠CAD=∠ACE
在△CAD与△ACE中
$\left\{\begin{array}{l}{∠CAD=∠ACE}\\{AC=CA}\\{∠D=∠E}\end{array}\right.$,
∴△CAD≌△ACE
∴CD=AE,
∵AE=AB,
∴CD=AB.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.下列说法中,正确的有( )
| A. | 过两点有无数条直线 | B. | 连结两点的线段叫做两点的距离 | ||
| C. | 两点之间,线段最短 | D. | AB=BC,则点B是线段AC的中点 |
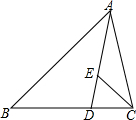 在△ABC中,∠B=45°,点D在边BC上,AD=AC,点E在边AD上,∠BCE=45°,若AB=5$\sqrt{2}$.AE=2DE,则AC=$\sqrt{26}$.
在△ABC中,∠B=45°,点D在边BC上,AD=AC,点E在边AD上,∠BCE=45°,若AB=5$\sqrt{2}$.AE=2DE,则AC=$\sqrt{26}$.
 如图,一座拱桥的轮廓是抛物线型,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加2$\sqrt{6}$-4m.
如图,一座拱桥的轮廓是抛物线型,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加2$\sqrt{6}$-4m.