题目内容
19．关于x的一元二次方程x2-2mx+（m-1）2=0有两个相等的实数根．（1）求m的值；
（2）求此方程的根．
分析 （1）由方程有两个相等的实数根结合根的判别式，即可得出△=8m-4=0，解之即可得出结论；
（2）将m的值代入原方程，利用配方法解方程即可得出结论．
解答 解：（1）∵关于x的一元二次方程x2-2mx+（m-1）2=0有两个相等的实数根，
∴△=（-2m）2-4（m-1）2=8m-4=0，
解得：m=$\frac{1}{2}$．
（2）将m=$\frac{1}{2}$代入原方程得x2-x+$\frac{1}{4}$=（x-$\frac{1}{2}$）2=0，
解得：x1=x2=$\frac{1}{2}$．
点评 本题考查了根的判别式以及配方法解一元二次方程，解题的关键是：（1）牢记“当△=0时，方程有两个相等的实数根”；（2）代入m的值，再解一元二次方程．
练习册系列答案
相关题目
9．当b＞0时，一次函数y=x+b的图象大致是（ ）
| A． |  | B． |  | C． |  | D． |  |
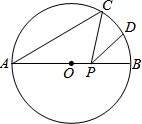如图，AB是⊙O的直径，AB=10，∠A=40°，点D为弧BC的中点，点P是直径AB上的一个动点，PC+PD的最小值为5$\sqrt{3}$．
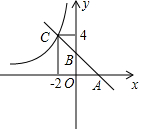如图，一条直线分别交x轴、y轴于A、B两点，交反比例函数y=$\frac{m}{x}$（m≠0）位于第二象限的一支于C点，OA=OB=2．