题目内容
20.先化简,后求值:$(\frac{x}{x-2}-\frac{4}{{{x^2}-2x}})÷\frac{x+2}{{{x^2}-x}}$,其中x满足x2-x-2=0.分析 先把括号内通分,再把分子分母因式分解和除法运算化为乘法运算,接着约分得到原式=x+1,然后利用因式分解法解x2-x-2=0,再利用分式有意义的条件把满足题意的x的值代入计算即可.
解答 解:原式=$\frac{{x}^{2}-4}{x(x-2)}$•$\frac{x(x-1)}{x+2}$
=$\frac{(x+2)(x-2)}{x(x-2)}$•$\frac{x(x-1)}{x+2}$
=x-1,
解方程x2-x-2=0,得x1=-1,x2=2,
当x=2时,原分式无意义,
所以当x=-1时,原式=-1-1=-2.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.注意分式有意义的条件.

练习册系列答案
相关题目
15.如表是我市4个区县今年5月31日最高气温(℃)的统计结果:
该日最高气温的众数和中位数分别是( )
| 永定区 | 武陵源区 | 慈利县 | 桑植县 |
| 32 | 32 | 33 | 30 |
| A. | 32℃,32℃ | B. | 32℃,33℃ | C. | 33℃,33℃ | D. | 32℃,30℃ |




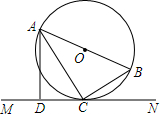 如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.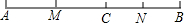 如图,点C在线段AB上,AC=8cm,CB=6cm,点M,N分别是AC,BC的中点.求线段MN的长.
如图,点C在线段AB上,AC=8cm,CB=6cm,点M,N分别是AC,BC的中点.求线段MN的长.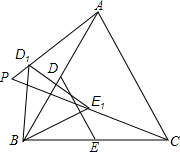 已知:在等边△ABC中,AB=2$\sqrt{3}$,D、E分别是AB,BC的中点(如图),若将△BDE绕点B逆时针旋转,得到△BD1E1.设旋转的角为α(0°<α<180°),记射线CE1与AD1的交点为P,点P到BC所在直线的距离的最大值为2.
已知:在等边△ABC中,AB=2$\sqrt{3}$,D、E分别是AB,BC的中点(如图),若将△BDE绕点B逆时针旋转,得到△BD1E1.设旋转的角为α(0°<α<180°),记射线CE1与AD1的交点为P,点P到BC所在直线的距离的最大值为2.