Question

5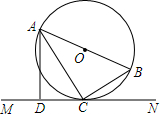．如图，AB是⊙O的直径，C是⊙O上的一点，直线MN经过点C，过点A作直线MN的垂线，垂足为点D，且∠BAC=∠CAD．
（1）求证：直线MN是⊙O的切线；
（2）若CD=3，∠CAD=30°，求⊙O的半径．

Answer 1

分析 （1）连接OC，推出AD∥OC，推出OC⊥MN，根据切线的判定推出即可；
（2）求出AD、AC长，证△ADC∽△ACB，得出比例式，代入求出AB长即可．

解答 （1）证明：连接OC，
因为OA=OC，
所以∠BAC=∠ACO．
因为AC平分∠BAD，
所以∠BAC=∠CAD，
故∠ACO=∠CAD．
所以OC∥AD，
又已知AD丄MN，
所以OC丄MN，
所以，直线MN是⊙O的切线；
（2）解：已知AB是⊙O的直径，则∠ACB=90°，
又AD丄MN，
则∠ADC=90°．
因为CD=3，∠CAD=30°，
所以AD=3$\sqrt{3}$，AC=6
在Rt△ABC和Rt△ACD中，∠BAC=∠CAD，
所以Rt△ABC∽Rt△ACD，
则$\frac{AB}{AC}=\frac{AC}{AD}$，
则AB=4$\sqrt{3}$，
所以⊙O的半径为2$\sqrt{3}$．

点评 本题考查了切线的判定，等腰三角形的判定和性质，平行线性质，相似三角形的性质和判定的应用，主要考查学生运用定理进行推理和计算的能力．