题目内容
按如下程序进行运算：
并规定，程序运行到“结果是否大于65”为一次运算，且运算进行3次才停止．则可输入的整数x的个数是（ ）
并规定，程序运行到“结果是否大于65”为一次运算，且运算进行3次才停止．则可输入的整数x的个数是（ ）
| A、5个 | B、6个 | C、7个 | D、8个 |
考点：一元一次不等式的应用
专题：图表型
分析：根据程序可以列出不等式组，即可确定x的整数值，从而求解．
解答：解：根据题意得：第一次：2x-1，
第二次：2（2x-1）-1=4x-3，
第三次：2（4x-3）-1=8x-7，
根据题意得：
，
解得：9＜x≤17．
则x的整数值是：10，11，12，13，14，15，16，17．
共有9个．
故选D．
第二次：2（2x-1）-1=4x-3，
第三次：2（4x-3）-1=8x-7，
根据题意得：
|
解得：9＜x≤17．
则x的整数值是：10，11，12，13，14，15，16，17．
共有9个．
故选D．
点评：本题考查了一元一次不等式的应用，解答本题的关键是正确理解题意，列出不等式组．
练习册系列答案
阅读快车系列答案
相关题目
如图，直线a，b被直线c所截，现给出四个条件：下列分解因式正确的是（ ）
| A、3x2-6x=x（3x-6） |
| B、a2-b2=（a+b）（a-b） |
| C、4x2-y2=（4x+y）（4x-y） |
| D、4x2-2xy+y2=（2x-y）2 |
关于x的方程x2-3x+c=0有实数根，则整数c的最大值为（ ）
| A、3 | B、2 | C、1 | D、0 |
下面几个结论：
（1）多边形每增加一条边，内角和增加180°；
（2）三角形外角和与任意一个凸多边形的外角和相等；
（3）任意一个凸多边形的内角中锐角的个数不能多于三个；
（4）任意凸n边形的对角线有
条．
其中正确的有（ ）个．
（1）多边形每增加一条边，内角和增加180°；
（2）三角形外角和与任意一个凸多边形的外角和相等；
（3）任意一个凸多边形的内角中锐角的个数不能多于三个；
（4）任意凸n边形的对角线有
| n(n-1) |
| 2 |
其中正确的有（ ）个．
| A、1 | B、2 | C、3 | D、4 |
如图，有下列结论，其中错误的是（ ）| A、∠A＞∠ACD |
| B、∠B+∠ACB=180°-∠A |
| C、∠A+∠ACB＜180° |
| D、∠HEC＞∠B |
实数
的值等于（ ）
| 16 |
| A、±4 | B、±2 | C、4 | D、2 |
计算x5•x5的值为（ ）
| A、x5 |
| B、x10 |
| C、x25 |
| D、2x5 |
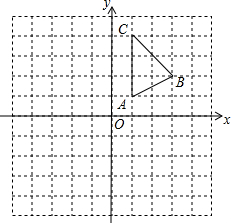在平面直角坐标系中，△ABC的三个顶点坐标分别为：A（1，1），B（3，2），C（1，4）．