题目内容
1.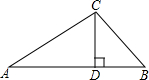 在△ABC中,∠A=30°,∠B=45°,CD⊥AB,垂足为D,CD=6,求AB的长.
在△ABC中,∠A=30°,∠B=45°,CD⊥AB,垂足为D,CD=6,求AB的长.
分析 根据含30度角直角三角形的性质求出AC,根据勾股定理求出AD,根据等腰直角三角形的性质和判定求出BD,即可求出AB.
解答  解:∵CD⊥AB,
解:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∵∠A=30°,CD=6,
∴AC=2CD=12,
由勾股定理得:AD=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$,
∵∠BDC=90°,∠B=45°,
∴∠BCD=45°=∠B,
∴BD=DC=6,
∴AB=6$\sqrt{3}$+6.
点评 本题考查了解直角三角形,含30度角的直角三角形,勾股定理等知识点的应用.解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
11.下列说法正确的是( )
| A. | 带正号的数是正数,带负号的数是负数 | |
| B. | 若|a|=a,则a一定是非负数 | |
| C. | 一个数的相反数,不是正数,就是负数 | |
| D. | 零除以任何数都等于零 |
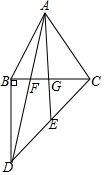 如图,在△ABC中,AB=AC,过点B作BD⊥BC,BD=BC,连接AD交BC于点F.E是CD的中点,连接AE交BC于G.
如图,在△ABC中,AB=AC,过点B作BD⊥BC,BD=BC,连接AD交BC于点F.E是CD的中点,连接AE交BC于G. 如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,判断∠BAC,∠B,∠E之间的关系,并说明理由.
如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,判断∠BAC,∠B,∠E之间的关系,并说明理由.