题目内容
19．
如图，△ABC的面积为18，BD=2DC，AE=EC，那么阴影部分的面积是$\frac{21}{5}$．
分析 根据BD=2DC，AE=EC可设△DFC的面积为x，△EFC的面积为y，则△BFD的面积为2x，△AEF的面积为y，再列出关于x、y的方程，求出x+y的值即可．
解答 
解：连接CF，
∵BD=2DC，AE=EC，
∴设△DFC的面积为x，△EFC的面积为y，则△BFD的面积为2x，△AEF的面积为y，
∵△BEC的面积=$\frac{1}{2}$S△ABC=9，
∴3x+y=9 ①，
∵△ADC的面积=$\frac{1}{3}$S△ABC=6，
∴x+2y=6 ②
①+2×②，可得x+y=$\frac{21}{5}$．
故答案为：$\frac{21}{5}$．
点评 本题考查的是三角形的面积，解题的关键是正确作出辅助线，利用三角形面积的性质求解．
练习册系列答案
相关题目
7．
由五个相同的正方体搭成的几何体如图所示，则它的俯视图是（ ）
由五个相同的正方体搭成的几何体如图所示，则它的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
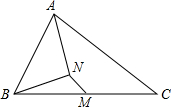如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，且AB=10，BC=15，MN=3，则AC的长是（ ）
4．
如图，在?ABCD中，AB=2，BC=4，∠D=60°，点P、Q分别是AC和BC上的动点，在点P和点Q运动的过程中，PB+PQ的最小值为（ ）
如图，在?ABCD中，AB=2，BC=4，∠D=60°，点P、Q分别是AC和BC上的动点，在点P和点Q运动的过程中，PB+PQ的最小值为（ ）| A． | 4 | B． | 3 | C． | 2$\sqrt{3}$ | D． | 4$\sqrt{3}$ |