Question

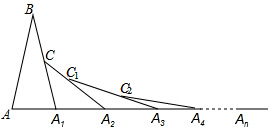如图，已知AB=A₁B，在AA₁的延长线上依次取A₂、A₃、A₄、…、A_n，并依次在三角形的外部作等腰三角形，使A₁C₁=A₁A₂，A₂C₂=A₂A₃，A₃C₃=A₃A₄，…，A_n-1C_n-1=A_n-1A_n，若∠B=30°，则∠A_n=

 

°．

Answer 1

考点：等腰三角形的性质

专题：规律型

分析：先根据等腰三角形的性质求出∠BA₁A的度数，再根据三角形外角的性质及等腰三角形的性质分别求出∠CA₂A₁，∠C₁A₃A₂及∠C₂A₄A₃…的度数，从而找出规律即可得出∠A_n的度数．

解答：解：∵在△ABA₁中，∠B=30°，AB=A₁B，
∴∠BA₁A=

180°-∠A

2

=

180°-30°

2

=75°，
∵A₁A₂=A₁C，∠BA₁A是△A₁A₂C的外角，
∴∠CA₂A₁=

∠BA1A

2

=

75°

2

=37.5°；
∴∠C₁A₃A₂=18，75°，∠C₂A₄A₃=9.375°，…，
∴∠A_n=

75°

2n-1

，
故答案为：

75°

2n-1

．

点评：本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出∠CA₂A₁，∠C₁A₃A₂及∠C₂A₄A₃…的度数，找出规律是解答此题的关键．