题目内容
 如图,AB是⊙O的直径,C,P是
如图,AB是⊙O的直径,C,P是 |
| AB |
(1)如图1,若点P是
 |
| AB |
(2)如图2,若点P是
 |
| BC |
考点:圆周角定理,全等三角形的判定与性质,勾股定理,圆心角、弧、弦的关系
专题:计算题
分析:(1)连结PB,如图1,根据圆周角定理得到∠APB=90°,根据圆心角、弧、弦的关系由
=
得到PA=PB,则△PAB为等腰直角三角形,所以PA=
AB=5
;
(2)连结BC、BP、PO,OP交BC于H,根据圆周角定理得,∠APB=∠ACB=90°,再根据垂径定理得OP⊥BC,则OH=
AC=3,在Rt△OBH中利用勾股定理计算出BH=4,在Rt△PBH中计算出PB=2
,然后在Rt△ABP中利用勾股定理可计算出PB=4
.
 |
| PA |
 |
| PB |
| ||
| 2 |
| 2 |
(2)连结BC、BP、PO,OP交BC于H,根据圆周角定理得,∠APB=∠ACB=90°,再根据垂径定理得OP⊥BC,则OH=
| 1 |
| 2 |
| 5 |
| 5 |
解答:解:(1)
 连结PB,如图1,
连结PB,如图1,
∵AB是⊙O的直径,
∴∠APB=90°,
∵点P是
的中点,
∴
=
,
∴PA=PB,
∴△PAB为等腰直角三角形,
∴PA=
AB=
×10=5
;
(2)连结BC、BP、PO,OP交BC于H,如图2,
∵AB是⊙O的直径,
∴∠APB=∠ACB=90°,
∵点P是
的中点,
∴OP⊥BC,
∴BH=CH,
∴OH=
AC=3,
在Rt△OBH中,∵OB=5,OH=3,
∴BH=
=4,
在Rt△PBH中,∵PH=OP-OH=5-3=2,BH=4,
∴PB=
=2
,
在Rt△ABP中,∵AB=10,PB=2
,
∴PA=
=4
.

 连结PB,如图1,
连结PB,如图1,∵AB是⊙O的直径,
∴∠APB=90°,
∵点P是
 |
| AB |
∴
 |
| PA |
 |
| PB |
∴PA=PB,
∴△PAB为等腰直角三角形,
∴PA=
| ||
| 2 |
| ||
| 2 |
| 2 |
(2)连结BC、BP、PO,OP交BC于H,如图2,
∵AB是⊙O的直径,
∴∠APB=∠ACB=90°,
∵点P是
 |
| BC |
∴OP⊥BC,
∴BH=CH,
∴OH=
| 1 |
| 2 |
在Rt△OBH中,∵OB=5,OH=3,
∴BH=
| OB2-OH2 |
在Rt△PBH中,∵PH=OP-OH=5-3=2,BH=4,
∴PB=
| PH2+BH2 |
| 5 |
在Rt△ABP中,∵AB=10,PB=2
| 5 |
∴PA=
| AB2-PB2 |
| 5 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了勾股定理.

练习册系列答案
相关题目
单项式22pm2n2的次数是( )
| A、4 | B、5 | C、6 | D、7 |
已知水星的半径约为24 400 000m,该数据用科学记数法表示为( )
| A、0.244×108m |
| B、2.44×106m |
| C、2.44×107m |
| D、24.4×106m |
-3的相反数和倒数分别为( )
| A、3,3 | ||
B、3,-
| ||
C、-
| ||
| D、以上都不对 |
抛物线y=x2-mx-m2+1的图象过原点,则m为( )
| A、0 | B、1 | C、-1 | D、±1 |

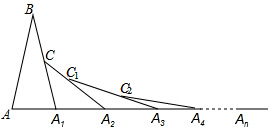 如图,已知AB=A1B,在AA1的延长线上依次取A2、A3、A4、…、An,并依次在三角形的外部作等腰三角形,使A1C1=A1A2,A2C2=A2A3,A3C3=A3A4,…,An-1Cn-1=An-1An,若∠B=30°,则∠An=
如图,已知AB=A1B,在AA1的延长线上依次取A2、A3、A4、…、An,并依次在三角形的外部作等腰三角形,使A1C1=A1A2,A2C2=A2A3,A3C3=A3A4,…,An-1Cn-1=An-1An,若∠B=30°,则∠An=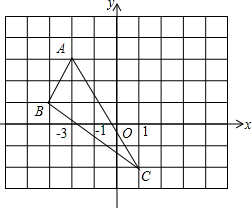 如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).
如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).