题目内容
先化简:-
÷(
-
),再求当x满足x2-2x-2=0时,此分式的值.
| 1 |
| x |
| x+1 |
| x2-x |
| x |
| x2-2x+1 |
考点:分式的化简求值
专题:
分析:先根据题意得出(x-1)2=3,再由分式混合运算的法则把原式进行化简,把(x-1)2=3代入进行计算即可.
解答:解:∵x2-2x-2=0,
∴(x-1)2=3,
原式=-
÷(
-
)
=-
÷
=-
÷
=
•x(x-1)2
=(x-1)2.
∴当(x-1)2=3时,原式=3.
∴(x-1)2=3,
原式=-
| 1 |
| x |
| x+1 |
| x(x-1) |
| x |
| (x-1)2 |
=-
| 1 |
| x |
| (x+1)(x-1)-x2 |
| x(x-1)2 |
=-
| 1 |
| x |
| -1 |
| x(x-1)2 |
=
| 1 |
| x |
=(x-1)2.
∴当(x-1)2=3时,原式=3.
点评:本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
反比例函数y=
,当x<0时,y随x的增大而减小,则k的取值范围为( )
| 2k+4 |
| x |
| A、k>0 | B、k<0 |
| C、k>-2 | D、k<-2 |
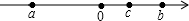 表示a、b、c三个数的点在数轴上对应的位置如图所示,则化简代数式|a-b|-|a-c|-|b+c|-|abc|结果是( )
表示a、b、c三个数的点在数轴上对应的位置如图所示,则化简代数式|a-b|-|a-c|-|b+c|-|abc|结果是( )| A、-2a+abc |
| B、2b-abc |
| C、2c-abc |
| D、-2c+abc |

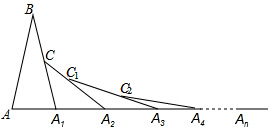 如图,已知AB=A1B,在AA1的延长线上依次取A2、A3、A4、…、An,并依次在三角形的外部作等腰三角形,使A1C1=A1A2,A2C2=A2A3,A3C3=A3A4,…,An-1Cn-1=An-1An,若∠B=30°,则∠An=
如图,已知AB=A1B,在AA1的延长线上依次取A2、A3、A4、…、An,并依次在三角形的外部作等腰三角形,使A1C1=A1A2,A2C2=A2A3,A3C3=A3A4,…,An-1Cn-1=An-1An,若∠B=30°,则∠An=