题目内容
四条线段的长分别是5cm,6cm,8cm,13cm,以其中任意三条线段为边可以构成______个三角形.
 2
【解析】首先发现每三条可以组合为5、6、8;5、6、13;5、8、13;6、8、13;
再根据三角形的三边关系,可知能构成三角形的为:5、6、8和6、8、13.
因此可构成2个三角形.
故答案为:2.
2
【解析】首先发现每三条可以组合为5、6、8;5、6、13;5、8、13;6、8、13;
再根据三角形的三边关系,可知能构成三角形的为:5、6、8和6、8、13.
因此可构成2个三角形.
故答案为:2.
练习册系列答案
相关题目
如图,从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式为h=30t-5t2,那么小球从抛出至回落到地面所需要的时间是( )
A. 6s B. 4s C. 3s D. 2s
 A
【解析】试题分析:由小球高度h与运动时间t的关系式h=30t﹣5t2,令h=0,解得的两值之差便是所要求得的结果.
由小球高度h与运动时间t的关系式h=30t﹣5t2. 令h=0,﹣5t2+30t=0 解得:t1=0,t2=6
△t=6,小球从抛出至回落到地面所需要的时间是6秒.
A
【解析】试题分析:由小球高度h与运动时间t的关系式h=30t﹣5t2,令h=0,解得的两值之差便是所要求得的结果.
由小球高度h与运动时间t的关系式h=30t﹣5t2. 令h=0,﹣5t2+30t=0 解得:t1=0,t2=6
△t=6,小球从抛出至回落到地面所需要的时间是6秒. 如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
A. 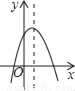 B.
B. 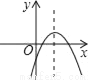 C.
C. 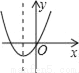 D.
D. 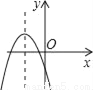
 B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B.
B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B. 已知一直角边和这条直角边的对角,求作直角三角形(用尺规作图,不写作法,但要保留作图痕迹).
 见解析
【解析】试题分析:根据题意写出已知和求作,然后再画出图形即可.
试题解析:已知:线段a和∠α,如下图(1).
求作:Rt△ABC,使BC=a,∠C=90?,∠A=∠α.
作法:(1)作∠α的余角∠β.
(2)作∠MBN=∠β.
(3)在射线BM上截取BC=a.
(4)过点C作CA⊥BM,交BN于点A,如图(2).
△ABC就是所求的直角三角形...
见解析
【解析】试题分析:根据题意写出已知和求作,然后再画出图形即可.
试题解析:已知:线段a和∠α,如下图(1).
求作:Rt△ABC,使BC=a,∠C=90?,∠A=∠α.
作法:(1)作∠α的余角∠β.
(2)作∠MBN=∠β.
(3)在射线BM上截取BC=a.
(4)过点C作CA⊥BM,交BN于点A,如图(2).
△ABC就是所求的直角三角形... △ABC中,AB=5,BC=3,则中线BD的取值范围是_________.
 1<BD<4
【解析】延长BD到E,使BD=DE,连接AE,如图:
∵BD是△ABC中线,
∴AD=DC,
在△BDC和△EDA中,
∵,
∴△BDC≌△EDA.
∴BC=AE=3,
∵在△ABE中,根据三角形的三边关系定理得:5+3>BE>5-3,
∴2<2BD<8,
即1<BD<4.
故答案为:1<BD<4.
1<BD<4
【解析】延长BD到E,使BD=DE,连接AE,如图:
∵BD是△ABC中线,
∴AD=DC,
在△BDC和△EDA中,
∵,
∴△BDC≌△EDA.
∴BC=AE=3,
∵在△ABE中,根据三角形的三边关系定理得:5+3>BE>5-3,
∴2<2BD<8,
即1<BD<4.
故答案为:1<BD<4. 三角形内有一点,它到三边的距离相等,则这点是该三角形的( )
A. 三条中线交点 B. 三条角平分线交点
C. 三条高线交点 D. 三条高线所在直线交点
 B
【解析】根据三角形角平分线上的点到角的两边的距离相等可得此点为角平分线的交点.
故选:B.
B
【解析】根据三角形角平分线上的点到角的两边的距离相等可得此点为角平分线的交点.
故选:B. 已知a+b=3,ab=2,求代数式a3b+2a2b2+ab3的值.
 18
【解析】试题分析:先提取公因式ab,再根据完全平方公式进行二次分解,然后代入数据进行计算即可得解.
【解析】
a3b+2a2b2+ab3
=ab(a2+2ab+b2)
=ab(a+b)2,
将a+b=3,ab=2代入得,ab(a+b)2=2×32=18.
故代数式a3b+2a2b2+ab3的值是18.
18
【解析】试题分析:先提取公因式ab,再根据完全平方公式进行二次分解,然后代入数据进行计算即可得解.
【解析】
a3b+2a2b2+ab3
=ab(a2+2ab+b2)
=ab(a+b)2,
将a+b=3,ab=2代入得,ab(a+b)2=2×32=18.
故代数式a3b+2a2b2+ab3的值是18. 已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5).
(1)求该二次函数的解析式;
(2)求该二次函数图象与坐标轴的交点坐标;
 (1)二次函数的关系式是y=-(x+1)2+4;(2)交点坐标是(-3,0)、(1,0)
【解析】试题分析:
(1)由题意可设二次函数解析式为,代入点B的坐标(2,-5)求出的值,即可得到二次函数的解析式;
(2)在(1)中所求函数解析式中,由时,求得对应的函数值即可得到函数图象与轴的交点坐标;由可得一元二次方程,解方程即可求得二次函数的图象与轴的交点坐标.
试题解析:
...
(1)二次函数的关系式是y=-(x+1)2+4;(2)交点坐标是(-3,0)、(1,0)
【解析】试题分析:
(1)由题意可设二次函数解析式为,代入点B的坐标(2,-5)求出的值,即可得到二次函数的解析式;
(2)在(1)中所求函数解析式中,由时,求得对应的函数值即可得到函数图象与轴的交点坐标;由可得一元二次方程,解方程即可求得二次函数的图象与轴的交点坐标.
试题解析:
... 阅读下列材料:
解答“已知 ,试确定
,试确定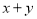 的取值范围”有如下解法:
的取值范围”有如下解法:
【解析】
∵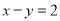 ,∴x=y+2,又∵
,∴x=y+2,又∵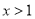 ,∴
,∴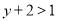 ,即
,即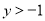
又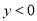 ,∴
,∴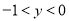 .…①
.…①
同理得: 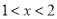 .…②
.…②
由①+②得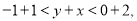
∴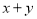 的取值范围是
的取值范围是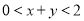 .
.
请按照上述方法,完成下列问题 :
已知关于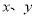 的方程组
的方程组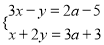 的解都是正数.
的解都是正数.
(1)求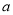 的取值范围;
的取值范围;
(2)已知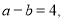 且
且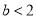 ,求
,求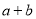 的取值范围;
的取值范围;
(3) 已知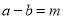 (
(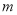 是大于0的常数),且
是大于0的常数),且 的最大值.(用
的最大值.(用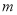 含的式子表示)
含的式子表示)
 (1);(2)(3)
【解析】(1 ) x=a-1, y=a+2(2分) (3分)
(2) 1
(1);(2)(3)
【解析】(1 ) x=a-1, y=a+2(2分) (3分)
(2) 1
