题目内容
3.已知点A($\frac{13}{4}$,y1),B($\frac{15}{4}$,y2)都在y=-$\frac{1}{3}$(x-4)2+1的抛物线上,则y1与y2的大小关系为y1<y2.分析 分别计算自变量为$\frac{13}{4}$和$\frac{15}{4}$所对应的函数值,然后比较函数值的大小即可.
解答 解:当x=$\frac{13}{4}$时,y1=-$\frac{1}{3}$($\frac{13}{4}$-4)2+1=$\frac{13}{16}$,
当x=$\frac{15}{4}$时,y2=-$\frac{1}{3}$($\frac{15}{4}$-4)2+1=$\frac{47}{48}$,
所以y1<y2.
故答案为y1<y2.
点评 本题考查了二次函数图象上点的坐标特征:解决此类问题就是把点的坐标代入抛物线解析式得到未知字母的方程,然后解方程求出字母的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD=( )
如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD=( )
 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD=( )
如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD=( )| A. | 128° | B. | 100° | C. | 64° | D. | 32° |
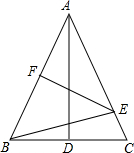 如图,AD和EF分别是△ABC中BC与AB垂直平分线,且BE+CE=20cm,则AB=20cm.
如图,AD和EF分别是△ABC中BC与AB垂直平分线,且BE+CE=20cm,则AB=20cm.