题目内容
15.(x+1)(x2-5ax+a)的乘积中不含x2项,求a的值.分析 先根据多项式乘以多项式法则展开,合并同类项,根据已知的方程-5a+1=0,求出即可.
解答 解:(x+1)(x2-5ax+a)
=x3-5ax2+ax+x2-5ax+a
=x3+(-5a+1)x2-4ax+a,
∵(x+1)(x2-5ax+a)的乘积中不含x2项,
∴-5a+1=0,
解得:a=$\frac{1}{5}$.
点评 本题考查了多项式乘以多项式法则,能正确根据多项式乘以多项式法则展开是解此题的关键.

练习册系列答案
相关题目
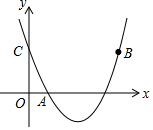 如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点A的坐标为(1,0),点B是点C关于该函数图象对称轴对称的点.
如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点A的坐标为(1,0),点B是点C关于该函数图象对称轴对称的点.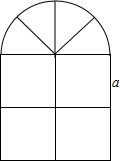 王军同学设计一个窗户模型,形状如图所示,(图中长度单位:cm)其中上部是半圆形,下部是边长相同的四个小正方形,已知下部每个小正方形的边长是acm.
王军同学设计一个窗户模型,形状如图所示,(图中长度单位:cm)其中上部是半圆形,下部是边长相同的四个小正方形,已知下部每个小正方形的边长是acm.