题目内容
8. 如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.(1)求证:PC是⊙O的切线;
(2)若PD=$\frac{16}{3}$cm,AC=8cm,点E是$\widehat{AB}$的中点,连接CE,求CE的长.
分析 (1)如图,连接OC,先利用切线的性质得到∠PAO=90°,在利用平行线的性质得到∠AOP=∠OBC,∠COP=∠OCB,接着证明△PAO≌△PCO 得到∠PAO=∠PCO=90°,然后根据切线的判定定理得到结论;
(2)连结EA、EB,作BH⊥CE于H,如图,利用圆周角定理得到∠ACB=∠AEB=90°,在利用平行线的性质和垂径定理得到AD=CD=$\frac{1}{2}$AC=4,则利用勾股定理计算出PA=$\frac{20}{3}$,接着证明Rt△PAD∽Rt△POA,利用相似比计算出PO=$\frac{25}{3}$,则OD=PO-PD=3,BC=2OD=6,于是利用勾股定理可计算出AB=10,接下来证明△BCH和△ABE都是等腰直角三角形,所以CH=BH=$\frac{\sqrt{2}}{2}$BC=3$\sqrt{2}$,BE=$\frac{\sqrt{2}}{2}$AB=5$\sqrt{2}$,然后利用勾股定理计算出EH即可得到CE的长.
解答 (1)证明:如图,连接OC,
∵PA切⊙O于A.
∴OA⊥PA,
∴∠PAO=90°,
∵OP∥BC,
∴∠AOP=∠OBC,∠COP=∠OCB,
∵OC=OB,
∴∠OBC=∠OCB,
∴∠AOP=∠COP,
在△PAO和△PCO中
$\left\{\begin{array}{l}{OA=OC}\\{∠AOP=∠COP}\\{OP=OP}\end{array}\right.$,
∴△PAO≌△PCO (SAS),
∴∠PAO=∠PCO=90°,
∴OC⊥PC,
∴PC是⊙O的切线;
(2)解:连结EA、EB,作BH⊥CE于H,如图,
∵AB是⊙O的直径,
∴∠ACB=∠AEB=90°,
∵OP∥BC,
∴PO⊥AC,
∴AD=CD=$\frac{1}{2}$AC=4,
在Rt△PAD中,PA=$\sqrt{P{D}^{2}+A{D}^{2}}$=$\sqrt{(\frac{16}{3})^{2}+{4}^{2}}$=$\frac{20}{3}$,
∵∠APO=∠DPA,
∴Rt△PAD∽Rt△POA,
∴PA:PO=PD:PA,即$\frac{20}{3}$:PO=$\frac{16}{3}$:$\frac{20}{3}$,解得PO=$\frac{25}{3}$,
∴OD=PO-PD=3,
∵AO=BO,OD∥BC,
∴BC=2OD=6,
在Rt△ACB中,AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵点E是$\widehat{AB}$的中点,
∴∠BCE=∠ACE=$\frac{1}{2}$∠ACB=45°,
∴AE=BE,
∴△BCH和△ABE都是等腰直角三角形,
∴CH=BH=$\frac{\sqrt{2}}{2}$BC=3$\sqrt{2}$,BE=$\frac{\sqrt{2}}{2}$AB=5$\sqrt{2}$,
在Rt△BEH中,EH=$\sqrt{(5\sqrt{2})^{2}-(3\sqrt{2})^{2}}$=4$\sqrt{2}$,
∴CE=CH+EH=3$\sqrt{2}$+4$\sqrt{2}$=7$\sqrt{2}$.
点评 本题考查了切线的判断与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线.常见的辅助线为:判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”; 有切线时,常常“遇到切点连圆心得半径”.解决(2)小题的关键是构建等腰直角三角形,把CE分为CH和EH进行计算.

 如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,顶点B的坐标为(4,6),直线y=kx+3k将平行四边形OABC分割成面积相等的两部分,则k的值是( )
如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,顶点B的坐标为(4,6),直线y=kx+3k将平行四边形OABC分割成面积相等的两部分,则k的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | -$\frac{3}{5}$ | D. | -$\frac{5}{3}$ |
| A. | m=-2,n=1 | B. | m=3,n=1 | C. | m=5,n=-1 | D. | 不能确定 |
| A. | x-3=2x | B. | x2-2=0 | C. | x2-2y=1 | D. | $\frac{1}{x}+1=2x$ |
| A. | x+$\frac{1}{y}$=2 | B. | xy+5=-4 | C. | 3x2+y=8 | D. | x+$\frac{y}{4}$=2 |
 如图,在Rt△ABC中,∠BAC=90°,延长BA到点D,使AD等于二分之一AB,点E,F分别为BC,AC的中点.
如图,在Rt△ABC中,∠BAC=90°,延长BA到点D,使AD等于二分之一AB,点E,F分别为BC,AC的中点.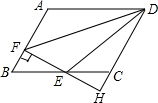 如图,在?ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则E到DF的距离是$\frac{2\sqrt{21}}{7}$.
如图,在?ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则E到DF的距离是$\frac{2\sqrt{21}}{7}$.