题目内容
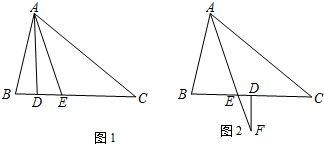
 如图,线段BC切⊙O于点C,以AC为直径,连接AB交⊙O于点D,点E是BC的中点,交AB于点D,连结OB、DE交于点F.
如图,线段BC切⊙O于点C,以AC为直径,连接AB交⊙O于点D,点E是BC的中点,交AB于点D,连结OB、DE交于点F.(1)求证:DE是⊙O的切线;
(2)若AC=4,BC=4
| 3 |
| EF |
| FD |
考点:切线的判定,勾股定理,相似三角形的判定与性质
专题:
分析:(1)连结OD、CD,则可得∠ODA=∠A,结合直径所对的圆周角为90°,可得∠ODE=90°,从而可证明OD⊥DE,也可得出结论;
(2)连结OE.根据三角形中位线定理得出OE∥AB,OE=
AB,由相似三角形的判定得到△OEF∽△BDF,则
=
.在Rt△ABC中,根据勾股定理求出AB=8,则OE=4,再证明△AOD是边长为2的等边三角形,得出AD=2,BD=AB-AD=6,进而求解即可.
(2)连结OE.根据三角形中位线定理得出OE∥AB,OE=
| 1 |
| 2 |
| EF |
| FD |
| OE |
| BD |
解答:(1)证明:连结OD、CD,如图.
∵AC是⊙O直径,
∴∠ADC=∠BDC=90°.
∵点E是BC的中点,
∴DE=BE=EC.
∵OA=OD,DE=BE,
∴∠ADO=∠A,∠DBE=∠BDE.
∵∠DBE+∠A=90°,
∴∠BDE+∠ADO=90°.
 ∴∠EDO=90°,
∴∠EDO=90°,
∴OD⊥DE,
即DE是⊙O的切线;
(2)解:连结OE.则OE∥AB,OE=
AB,
∴△OEF∽△BDF,
∴
=
.
∵BC切⊙O于点C,
∴∠ACB=90°.
在Rt△ABC中,AC=4,BC=4
,
根据勾股定理得,AB=8,
∴OE=4,
∵∠A=60°,
∴△AOD是边长为2的等边三角形,
∴AD=2,BD=AB-AD=6,
∴
=
=
=
.
∵AC是⊙O直径,
∴∠ADC=∠BDC=90°.
∵点E是BC的中点,
∴DE=BE=EC.
∵OA=OD,DE=BE,
∴∠ADO=∠A,∠DBE=∠BDE.
∵∠DBE+∠A=90°,
∴∠BDE+∠ADO=90°.
 ∴∠EDO=90°,
∴∠EDO=90°,∴OD⊥DE,
即DE是⊙O的切线;
(2)解:连结OE.则OE∥AB,OE=
| 1 |
| 2 |
∴△OEF∽△BDF,
∴
| EF |
| FD |
| OE |
| BD |
∵BC切⊙O于点C,
∴∠ACB=90°.
在Rt△ABC中,AC=4,BC=4
| 3 |
根据勾股定理得,AB=8,
∴OE=4,
∵∠A=60°,
∴△AOD是边长为2的等边三角形,
∴AD=2,BD=AB-AD=6,
∴
| EF |
| FD |
| OE |
| BD |
| 4 |
| 6 |
| 2 |
| 3 |
点评:本题考查了切线的判定,相似三角形的判定与性质,三角形中位线定理,勾股定理等知识.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
下列函数中,是一次函数但不是正比例函数的为( )
A、y=-
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
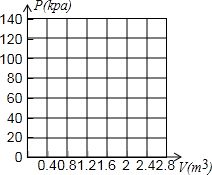 在研究气体压强和体积关系的物理实验中,一个气球内充满了一定质量的气体,实验中气体温度保持不变,实验人员记录了实验过程中气球内的气体压强p(kpa)与气体体积V(m3)的数据如下表:
在研究气体压强和体积关系的物理实验中,一个气球内充满了一定质量的气体,实验中气体温度保持不变,实验人员记录了实验过程中气球内的气体压强p(kpa)与气体体积V(m3)的数据如下表: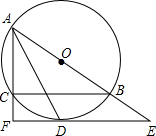 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作EF∥BC,EF与AB、AC的延长线分别交于点E、F.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作EF∥BC,EF与AB、AC的延长线分别交于点E、F.