题目内容
3．
已知，a、b在数轴上对应的点如图所示，则化简|a-b|-$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=0．
分析 根据数轴判断出a＞0，b＜0，然后根据绝对值的性质和二次根式的性质化简即可．
解答 解：由图可知，a＞0，b＜0，
所以，a-b＞0，
|a-b|-$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=a-b-a-（-b），
=a-b-a+b，
=0．
故答案为：0．
点评 本题考查了实数与数轴，是基础题，观察图形判断出a、b的正负情况是解题的关键．
练习册系列答案
相关题目
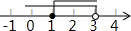
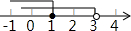
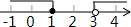
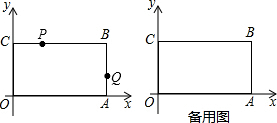
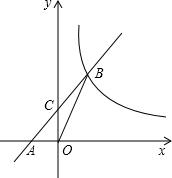如图，在平面直角坐标系中，直线y=k1x+2与x轴交于点A，与y轴交于点C，与反比例函数y=$\frac{{k}_{2}}{x}$在第一象限内的图象交于点B，连接BO，若S△OBC=1，tan∠BOC=$\frac{1}{3}$，求k2的值．
