题目内容
5．
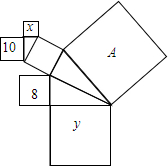如图，图中的所有三角形都是直角三角形，所有四边形都是正方形，正方形A的边长为$\sqrt{37}$，另外四个正方形中的数字8，x，10，y分别表示该正方形面积，则x与y的数量关系是x+y=19．
分析 先由正方形A的边长为$\sqrt{37}$，得出SA=37，再根据勾股定理的几何意义，得到x+10+（8+y）=SA，由此得出x与y的数量关系．
解答 解：∵正方形A的边长为$\sqrt{37}$，
∴SA=37，
根据勾股定理的几何意义，得x+10+（8+y）=SA=37，
∴x+y=37-18=19，即x+y=19．
故答案为x+y=19．
点评 本题考查了勾股定理的几何意义，要知道，以斜边边长为边长的正方形的面积是以两直角边边长为边长的正方形的面积之和．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
15．
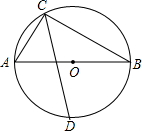如图，AB为⊙O直径，C为⊙O上一点，∠ACB的平方线交⊙O于点D，若AB=10，AC=6，则CD的长为（ ）
如图，AB为⊙O直径，C为⊙O上一点，∠ACB的平方线交⊙O于点D，若AB=10，AC=6，则CD的长为（ ）| A． | 7 | B． | 7$\sqrt{2}$ | C． | 8 | D． | 8$\sqrt{2}$ |
13．如图，甲、乙、丙三个三角形中和△ABC全等的图形是（ ）
| A． | 甲和乙 | B． | 乙和丙 | C． | 只有乙 | D． | 只有丙 |
20．
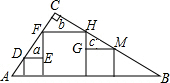如图，在Rt△ABC（∠C=90°）内有边长分别为a、b、c的三个正方形，下列结论一定成立的是（ ）
如图，在Rt△ABC（∠C=90°）内有边长分别为a、b、c的三个正方形，下列结论一定成立的是（ ）| A． | a+c=b | B． | ac=b2 | C． | a2+c2=b2 | D． | $\frac{1}{b}$+$\frac{1}{c}$=$\frac{1}{a}$ |
10．用一个平面去截一个圆锥，截面图形不可能是（ ）
| A． |  | B． |  | C． |  | D． |  |
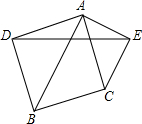如图，以△ABC的两边AB、AC为底边向外做等腰直角三角形ADB和ACE，连接DE，若S△ADE：S四边形DBCE=1：2，且tan∠AED=$\frac{3}{4}$，则$\frac{AB}{AC}$的值为$\frac{\sqrt{34}}{5}$．