题目内容
15.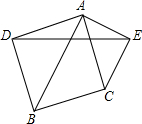 如图,以△ABC的两边AB、AC为底边向外做等腰直角三角形ADB和ACE,连接DE,若S△ADE:S四边形DBCE=1:2,且tan∠AED=$\frac{3}{4}$,则$\frac{AB}{AC}$的值为$\frac{\sqrt{34}}{5}$.
如图,以△ABC的两边AB、AC为底边向外做等腰直角三角形ADB和ACE,连接DE,若S△ADE:S四边形DBCE=1:2,且tan∠AED=$\frac{3}{4}$,则$\frac{AB}{AC}$的值为$\frac{\sqrt{34}}{5}$.
分析 过A作AH⊥DE于H,过B作BM⊥DE于M,过C作CN⊥DE于N,于是得到∠BMD=∠AHD=90°,根据等腰直角三角形的性质得到AD=BD,∠ADB=90°,于是得到∠DAH=∠BDM,推出△BDM≌△ADH,同理△CEN≌△AEH,由于S△ADE:S四边形DBCE=1:2,求得S△ADE=S梯形BCNM,根据梯形的面积公式得到AH•(DH+EH)=(BM+CN)•MN,证得AH=MN,由tan∠AED=$\frac{3}{4}$,设AH=3x,得到DM=EN=3x,EH=CN=4x,根据勾股定理求出AD=$\sqrt{34}$x,然后根据相似三角形的性质即可得到结论.
解答  解:过A作AH⊥DE于H,过B作BM⊥DE于M,过C作CN⊥DE于N,
解:过A作AH⊥DE于H,过B作BM⊥DE于M,过C作CN⊥DE于N,
∴∠BMD=∠AHD=90°,
∵△ABD是等腰直角三角形,
∴AD=BD,∠ADB=90°,
∴∠ADH+∠BDH=∠ADH+∠DAH=90°,
∴∠DAH=∠BDM,
在△BDM与△ADH中,
$\left\{\begin{array}{l}{∠BDH=∠DAH}\\{∠BMD=∠DHA}\\{AD=BD}\end{array}\right.$,
∴△BDM≌△ADH,
同理△CEN≌△AEH,
∵S△ADE:S四边形DBCE=1:2,
∴S△ADE=S梯形BCNM,
∴AH•(DH+EH)=(BM+CN)•MN,
∴AH=MN,
∵tan∠AED=$\frac{3}{4}$,
∴设AH=3x,
∴DM=EN=3x,EH=CN=4x,
∴HN=HE-NE=x,AE=5x,
∴MH=2x,
∴DH=DM+MH=5x,
∵AD2=DH2+AH2,
∴AD=$\sqrt{34}$x,
∵△ABD,△ACE是等腰直角三角形,
∴△ABD∽△ACE,
∴$\frac{AB}{AC}=\frac{AD}{AE}$=$\frac{\sqrt{34}}{5}$.
故答案为:$\frac{\sqrt{34}}{5}$.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 只有1,-7,+101,-9是整数 | B. | 其中有三个数是正整数 | ||
| C. | 非负数有1,8.6,0,$\frac{5}{6}$,+101 | D. | 只有-$\frac{4}{5}$,-4$\frac{2}{3}$是负分数 |
| A. | 4,5,6 | B. | 1,1,2 | C. | 8,15,17 | D. | 5,12,23 |
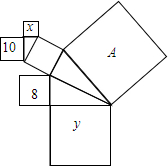 如图,图中的所有三角形都是直角三角形,所有四边形都是正方形,正方形A的边长为$\sqrt{37}$,另外四个正方形中的数字8,x,10,y分别表示该正方形面积,则x与y的数量关系是x+y=19.
如图,图中的所有三角形都是直角三角形,所有四边形都是正方形,正方形A的边长为$\sqrt{37}$,另外四个正方形中的数字8,x,10,y分别表示该正方形面积,则x与y的数量关系是x+y=19.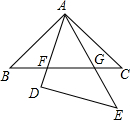 如图△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA 绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.
如图△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA 绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5. 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=6cm,则线段AC=24 cm.
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=6cm,则线段AC=24 cm.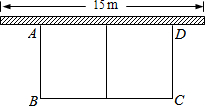 如图,某农场利用一面墙(墙长为15m)建养鸡场,用30m的围栏围成总面积为72m2的两个大小相同的矩形鸡圈,求养鸡场的两边AB,BC的长各为多少?
如图,某农场利用一面墙(墙长为15m)建养鸡场,用30m的围栏围成总面积为72m2的两个大小相同的矩形鸡圈,求养鸡场的两边AB,BC的长各为多少?