题目内容
15.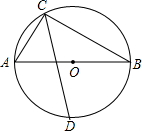 如图,AB为⊙O直径,C为⊙O上一点,∠ACB的平方线交⊙O于点D,若AB=10,AC=6,则CD的长为( )
如图,AB为⊙O直径,C为⊙O上一点,∠ACB的平方线交⊙O于点D,若AB=10,AC=6,则CD的长为( )| A. | 7 | B. | 7$\sqrt{2}$ | C. | 8 | D. | 8$\sqrt{2}$ |
分析 作DF⊥CA,交CA的延长线于点F,作DG⊥CB于点G,连接DA,DB.由CD平分∠ACB,根据角平分线的性质得出DF=DG,由HL证明△AFD≌△BGD,△CDF≌△CDG,得出CF=7,又△CDF是等腰直角三角形,从而求出CD.
解答 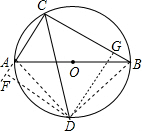 解:作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.
解:作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴DF=DG,弧AD=弧BD,
∴DA=DB.
在Rt△AFD和Rt△BGD中,
$\left\{\begin{array}{l}{BD=AD}\\{DF=DG}\end{array}\right.$,
∴△AFD≌△BGD(HL),
∴AF=BG.
在△CDF和△CDG中,
$\left\{\begin{array}{l}{∠ACD=∠GCD}\\{∠CFD=∠DGC}\\{CD=CD}\end{array}\right.$,
∴△CDF≌△CDG(AAS),
∴CF=CG.
∵AC=6,AB=10,
∴BC=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴AF=1,
∴CF=7,
∵△CDF是等腰直角三角形,
∴CD=7$\sqrt{2}$.
故选B.
点评 本题主要考查了圆周角的性质,圆心角、弧、弦的对等关系,全等三角形的判定,角平分线的性质等知识点的运用.关键是正确作出辅助线.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
3.在下列数:+(-3),-(-2.6),-(+5),+(+$\frac{1}{3}$)中,是负数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.以下列数组为边长,能构成直角三角形的是( )
| A. | 2,3,4 | B. | 1.3,1.4,1.5 | C. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | D. | 0.3,0.4,0.5 |
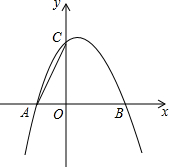 如图,二次函数y=-x2+bx+c的图象与x轴交于点A(-1,0),B(2,0),与y轴相交于点C.
如图,二次函数y=-x2+bx+c的图象与x轴交于点A(-1,0),B(2,0),与y轴相交于点C.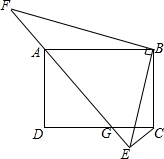 如图,在矩形ABCD中,AB=4,BC=3,G是CD边上的动点(点G不与点C、D重合),CE⊥AG的延长线于G点,BF⊥BE交EA的延长线于F点.
如图,在矩形ABCD中,AB=4,BC=3,G是CD边上的动点(点G不与点C、D重合),CE⊥AG的延长线于G点,BF⊥BE交EA的延长线于F点. 等腰△ABC中,腰长AB=8cm,BC=5cm,∠CBD=18°,AB的垂直平分线MN交AC于点D.
等腰△ABC中,腰长AB=8cm,BC=5cm,∠CBD=18°,AB的垂直平分线MN交AC于点D.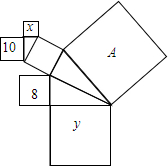 如图,图中的所有三角形都是直角三角形,所有四边形都是正方形,正方形A的边长为$\sqrt{37}$,另外四个正方形中的数字8,x,10,y分别表示该正方形面积,则x与y的数量关系是x+y=19.
如图,图中的所有三角形都是直角三角形,所有四边形都是正方形,正方形A的边长为$\sqrt{37}$,另外四个正方形中的数字8,x,10,y分别表示该正方形面积,则x与y的数量关系是x+y=19.