题目内容
5. 王老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)
王老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,如图,那么到达乙地时油
箱剩余油量是( )
| A. | 10升 | B. | 20升 | C. | 30升 | D. | 40升 |
分析 先运用待定系数法求出y与x之间的函数关系式,然后把x=240时代入解析式就可以求出y的值,从而得出剩余的油量.
解答 解:设y与x之间的函数关系式为y=kx+b,由函数图象,得
$\left\{\begin{array}{l}{b=35}\\{160k+b=25}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{16}}\\{b=35}\end{array}\right.$,
则y=-$\frac{1}{16}$x+35.
当x=240时,
y=-$\frac{1}{16}$×240+35=20(升).
故选:B.
点评 本题考查了运用待定系数法求一次函数的运用,根据自变量求函数值的运用,解答时理解函数图象的含义求出一次函数的解析式是关键.

练习册系列答案
相关题目
16.有下列四个结论:
①二次根式$\sqrt{b^2}$是非负数;
②若$\sqrt{{a^2}-1}=\sqrt{a+1}•\sqrt{a-1}$,则a的取值范围是a≥1;
③将m4-36在实数范围内分解因式,结果为(m2+6)(m+$\sqrt{6}$)(m-$\sqrt{6}$);
④当x>0时,$\sqrt{x}$<x,
其中正确的结论是( )
①二次根式$\sqrt{b^2}$是非负数;
②若$\sqrt{{a^2}-1}=\sqrt{a+1}•\sqrt{a-1}$,则a的取值范围是a≥1;
③将m4-36在实数范围内分解因式,结果为(m2+6)(m+$\sqrt{6}$)(m-$\sqrt{6}$);
④当x>0时,$\sqrt{x}$<x,
其中正确的结论是( )
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ①②③④ |
17.小明同学在广饶某电器超市进行社会实践活动时发现,该超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,近两周的销售情况如表所示:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第二周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
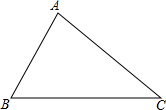 现有三个村庄A、B、C,位置如图所示,线段AB、BC、AC分别是连通两个村庄之间的公路.先要修一个水站P,使水站不仅到村庄A、C的距离相等,并且到公路AB、AC的距离也相等,请在图中作出水站P的位置.
现有三个村庄A、B、C,位置如图所示,线段AB、BC、AC分别是连通两个村庄之间的公路.先要修一个水站P,使水站不仅到村庄A、C的距离相等,并且到公路AB、AC的距离也相等,请在图中作出水站P的位置. 根据如图所示程序计算函数值,若输入的x值为$\frac{5}{2}$,则输出的函数值y为$\frac{2}{5}$.
根据如图所示程序计算函数值,若输入的x值为$\frac{5}{2}$,则输出的函数值y为$\frac{2}{5}$.