题目内容
10.(1)计算:$\frac{5}{\sqrt{5}}$-(2-$\sqrt{5}$)0+($\frac{1}{2}$)-2.(2)解分式方程:$\frac{x}{x-1}$+$\frac{2}{1-x}$=4.
分析 (1)本题涉及二次根式化简、零指数幂、负整数指数幂3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
(2)观察可得方程最简公分母为(x-1),将方程去分母转化为整式方程即可求解.
解答 解:(1)$\frac{5}{\sqrt{5}}$-(2-$\sqrt{5}$)0+($\frac{1}{2}$)-2
=$\sqrt{5}$-1+4
=$\sqrt{5}$+3;
(2)方程两边同乘(x-1),
得:x-2=4(x-1),
整理得:-3x=-2,
解得:x=$\frac{2}{3}$,
经检验x=$\frac{2}{3}$是原方程的解,
故原方程的解为x=$\frac{2}{3}$.
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.同时考查了解分式方程,解分式方程去分母时有常数项的注意不要漏乘,求解后要进行检验,这两项是都是容易忽略的地方,要注意检查.

练习册系列答案
相关题目
20.下列判断正确的是( )
| A. | “任意选择某一电视频道,它正在播放动画片”是必然事件 | |
| B. | 某运动员投一次篮,投中的概率为0.8,则该运动员投5次篮,一定有4次投中 | |
| C. | 任总抛掷一枚均匀的硬币,反面朝上的概率为$\frac{1}{2}$ | |
| D. | 布袋里有3个白球,1个黑球.任意取出1个球,恰好是黑球的概率是$\frac{1}{3}$ |
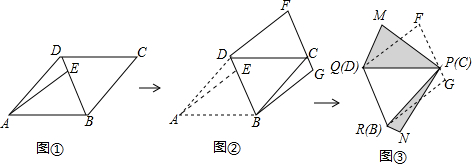
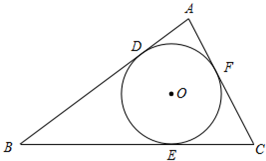 阅读下列材料并回答问题:
阅读下列材料并回答问题: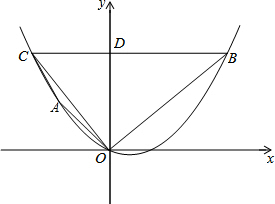 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx经过两点A(-1,1),B(2,2).过点B作BC∥x轴,交抛物线于点C,交y轴于点D.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx经过两点A(-1,1),B(2,2).过点B作BC∥x轴,交抛物线于点C,交y轴于点D. 如图,反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于点A(2,2)、B($\frac{1}{2}$,n).
如图,反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于点A(2,2)、B($\frac{1}{2}$,n). 二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=-$\frac{1}{2}$x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).
二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=-$\frac{1}{2}$x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).