题目内容
5.无论x取何值,代数式$\sqrt{4{x^2}-12x+m}$都有意义,则m的取值范围为m≥9.分析 根据二次根式有意义,被开方数大于等于0,再利用根的判别式△≤0列式计算即可得解.
解答 解:由题意得,4x2-12x+m≥0,
△=(-12)2-4×4×m≤0,
解得m≥9.
故答案为:m≥9.
点评 本题考查了二次根式有意义的条件,利用根的判别式列出不等式是解题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
20.下列调查中,①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“神舟9号”的成功发射,对其零部件进行检查;④调查运动员兴奋剂的使用情况.其中适合采用抽样调查的是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
17.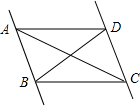 如图,给出下列四个条件:①∠DAC=∠ACB;②∠ABD=∠BDC;③∠BAD+∠CDA=180°;④∠ADC+∠BCD=180°.其中能判定AD∥BC的条件有( )
如图,给出下列四个条件:①∠DAC=∠ACB;②∠ABD=∠BDC;③∠BAD+∠CDA=180°;④∠ADC+∠BCD=180°.其中能判定AD∥BC的条件有( )
 如图,给出下列四个条件:①∠DAC=∠ACB;②∠ABD=∠BDC;③∠BAD+∠CDA=180°;④∠ADC+∠BCD=180°.其中能判定AD∥BC的条件有( )
如图,给出下列四个条件:①∠DAC=∠ACB;②∠ABD=∠BDC;③∠BAD+∠CDA=180°;④∠ADC+∠BCD=180°.其中能判定AD∥BC的条件有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.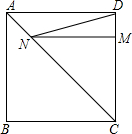 如图所示,正方形ABCD的边长为4,点M在边DC上,且DM=1,点N是边AC上一动点,则线段DN+MN的最小值为( )
如图所示,正方形ABCD的边长为4,点M在边DC上,且DM=1,点N是边AC上一动点,则线段DN+MN的最小值为( )
 如图所示,正方形ABCD的边长为4,点M在边DC上,且DM=1,点N是边AC上一动点,则线段DN+MN的最小值为( )
如图所示,正方形ABCD的边长为4,点M在边DC上,且DM=1,点N是边AC上一动点,则线段DN+MN的最小值为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{17}$ | D. | 5 |
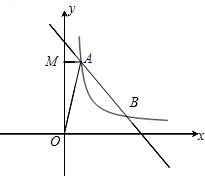 如图,一次函数y=mx+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,
如图,一次函数y=mx+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,
