题目内容
19.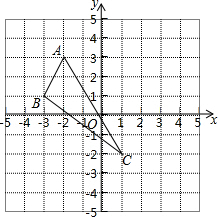 已知△ABC在平面直角坐标系中的位置如图所示
已知△ABC在平面直角坐标系中的位置如图所示(1)画出△ABC向右平移4个单位的△A′B′C′;
(2)求△A′B′C′的周长和面积各是多少?
分析 (1)首先找出A、B、C三点的对应点,再顺次连接即可;
(2)利用勾股定理计算出A′B′、A′C′、B′C′的长,再求周长即可;利用长方形的面积减去周围多与三角形的面积可得△A′B′C′的面积.
解答 解:(1)如图所示: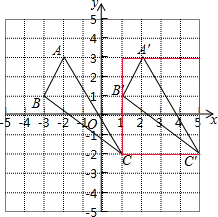 ;
;
(2)A′B′=$\sqrt{1+{2}^{2}}$=$\sqrt{5}$,C′B′=$\sqrt{{3}^{2}+{4}^{2}}$=5,A′C′=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$,
△A′B′C′的周长:$\sqrt{5}$+$\sqrt{34}$+5;
△A′B′C′的面积:4×5-$\frac{1}{2}×1×2$-$\frac{1}{2}×4×3$-$\frac{1}{2}×3×5$=20-1-6-7.5=5.5.
点评 此题主要考查了平移作图,以及勾股定理的应用,关键是掌握作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.

练习册系列答案
相关题目
10.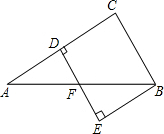 如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
 如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
4.下列等式成立的是( )
| A. | (a+b)2=a2+b2 | B. | (a-b)2=a2-b2 | C. | (x-4)(x+4)=x2-4 | D. | (a+b)2=a2+b2+2ab |
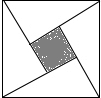 如图,“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,随机在大正方形及其内部区域投针,若针扎到小正方形(阴影部分)的概率是$\frac{1}{9}$,则大、小两个正方形的边长之比是3:1.
如图,“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,随机在大正方形及其内部区域投针,若针扎到小正方形(阴影部分)的概率是$\frac{1}{9}$,则大、小两个正方形的边长之比是3:1. 如图,圆内接四边形ABCD中,AB=AD,∠BAD=60°,则∠ACD度数是60°.
如图,圆内接四边形ABCD中,AB=AD,∠BAD=60°,则∠ACD度数是60°.