题目内容
13.如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,使点B旋转到B′点,则点B在两次旋转过程中经过的路径的长是( )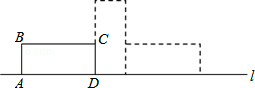
| A. | 25π | B. | $\frac{25}{4}$π | C. | $\frac{25}{2}$π | D. | $\frac{13}{2}$π |
分析 连接BD,B′D,首先根据勾股定理计算出BD长,再根据弧长计算公式计算出$\widehat{BB′}$,$\widehat{B′B″}$的长,然后再求和计算出点B在两次旋转过程中经过的路径的长即可.
解答  解:连接BD,B′D,
解:连接BD,B′D,
∵AB=5,AD=12,
∴BD=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∴$\widehat{BB′}$的长:$\frac{90π×13}{180}$=$\frac{13π}{2}$,
∵$\widehat{B′B″}$的长:$\frac{90π×12}{180}$=6π,
∴点B在两次旋转过程中经过的路径的长是:$\frac{13π}{2}$+6π=$\frac{25π}{2}$,
故选:C.
点评 此题主要考查了弧长计算,以及勾股定理的应用,关键是掌握弧长计算公式l=$\frac{nπr}{180}$.

练习册系列答案
相关题目
5.下列各项中叙述正确的是( )
| A. | 若mx=nx,则m=n | |
| B. | 若|x|-x=0,则x=0 | |
| C. | 若mx=nx,则 $\frac{2m}{{x}^{2015}+1}$=$\frac{2n}{{x}^{2015}+1}$ | |
| D. | 若m=n,则24-mx=24-nx |
2.五箱苹果的质量(单位:kg)分别为:19,20,21,22,19,则这五箱苹果质量的众数和中位数分别为( )
| A. | 21和19 | B. | 20和19 | C. | 19和19 | D. | 19和22 |




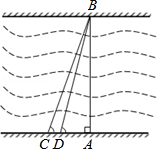 大河网报道“郑州东风渠再添4座新桥”,如图,某座桥的两端位于A,B两点,小华为了测量A、B之间的河宽,在垂直于桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=24米.求AB的长(精确到1米).
大河网报道“郑州东风渠再添4座新桥”,如图,某座桥的两端位于A,B两点,小华为了测量A、B之间的河宽,在垂直于桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=24米.求AB的长(精确到1米).