题目内容
5.下列各项中叙述正确的是( )| A. | 若mx=nx,则m=n | |
| B. | 若|x|-x=0,则x=0 | |
| C. | 若mx=nx,则 $\frac{2m}{{x}^{2015}+1}$=$\frac{2n}{{x}^{2015}+1}$ | |
| D. | 若m=n,则24-mx=24-nx |
分析 根据等式的性质进行解答并作出正确的判断.
解答 解:A、当x=0时,m=n不一定成立,故本选项错误;
B、|x|-x=0,则x=0或x=1,故本选项错误;
C、当x≠0且x≠-1时该等式成立,故本选项错误;
D、在等式m=n的两边同时乘以-x,然后加上24,等式仍成立,即24-mx=24-nx,故本选项正确.
故选:D.
点评 本题主要考查了等式的基本性质.
等式性质:1、等式的两边同时加上或减去同一个数或字母,等式仍成立;
2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.

练习册系列答案
相关题目
13.如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,使点B旋转到B′点,则点B在两次旋转过程中经过的路径的长是( )
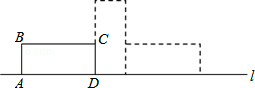

| A. | 25π | B. | $\frac{25}{4}$π | C. | $\frac{25}{2}$π | D. | $\frac{13}{2}$π |
17.下列运算正确的是( )
| A. | a2+2a3=3a5 | B. | -3a+2a=-a | C. | (3a3)2=6a6 | D. | a8÷a2=a4 |
 如图,在?ABCD中,AB=6,BC=8,AC=10.
如图,在?ABCD中,AB=6,BC=8,AC=10.
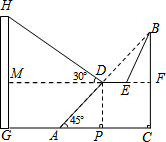 如图已知斜坡AB长60$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
如图已知斜坡AB长60$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).


