题目内容
若（x2-3x+4）（x2-ax+1）的展开式中，不含x2项，则a的值是 ．
考点：多项式乘多项式
专题：计算题
分析：原式利用多项式乘多项式法则计算，根据结果不含x2项，即可确定出a的值．
解答：解：（x2-3x+4）（x2-ax+1）=x4-ax+x2-3x3+3ax2-3x+4x2-4ax+4=x4-3x3+（1+3a+4）x2+（3-5a）x+4，
由结果不含x2项，得到1+3a+4=0，
解得：a=-
．
故答案为：-
．
由结果不含x2项，得到1+3a+4=0，
解得：a=-
| 5 |
| 3 |
故答案为：-
| 5 |
| 3 |
点评：此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
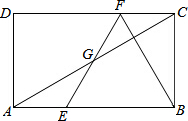如图，在矩形ABCD中，E、F分别是AB、CD上的点，AE=CF，连接EF、BF，EF交对角线AC于点G，若BE=BF，∠DFE=2∠BAC，BC=下列运算正确的是（ ）
| A、（3xy2）2=6x2y4 | ||
B、2x-1=
| ||
| C、（-x）7÷（-x2）=x5 | ||
| D、3x3+2x2=5x5 |