题目内容
18．
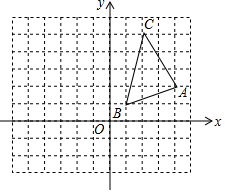△ABC在平面直角坐标系中的位置如图所示，其中A、B、C三点在格点上．（1）作△A1B1C1，使其与△ABC关于y轴对称．
（2）在x轴上有一点D能使AD与BD的长度之和最小，请直接写出点D的坐标（2，0）．
分析 （1）根据网格结构找出点A、B、C关于x轴的对称的A1、B1、C1的位置，然后顺次连接即可，再根据平面直角坐标系写出点C1的坐标；
（2）确定出点B关于x轴的对称点B′，根据轴对称确定最短路线问题连接AB′，与x轴的交点即为所求的点D，再写出坐标即可．
解答 
解：（1）△A1B1C1如图所示；
（2）点D如图所示，OD=2，
所以，点D的坐标为（2，0）．
故答案为：（2，0）．
点评 本题考查了利用轴对称变换作图，利用轴对称确定最短路线问题，熟练掌握网格结构准确找出对应点的位置是解题的关键．
练习册系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
8．在-0.25、+2.3、0、-$\frac{3}{2}$这四个数中，最小的数是（ ）
| A． | -0.25 | B． | +2.3 | C． | 0 | D． | -$\frac{3}{2}$ |
9．下列计算中去括号正确的是（ ）
| A． | -（5-2x）=2x-5 | B． | 7（a+3）=7a+3 | C． | -（a-b）=-a-b | D． | -（2x-5）=2x-5 |
6．下列方程中，是关于x的一元二次方程的是（ ）
| A． | x2+$\frac{1}{{x}^{2}}$=1 | B． | x2+3x-1=0 | C． | ax2+bx+c | D． | 3x+y=10 |
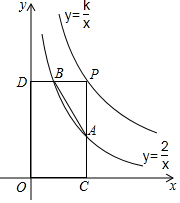两个反比例函数y=$\frac{2}{x}$和y=$\frac{k}{x}$（k＞2）在第一象限的图象如图所示，第一象限中的点P在y=$\frac{k}{x}$的图象上运动，PC⊥x轴于C，PD⊥y轴于D，PC、PD分别交y=$\frac{2}{x}$的图象于点A，B．
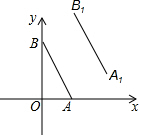如图，A、B的坐标分别为（2，0），（0，4），若将线段AB平移到A1B1，A1，B1的坐标分别为（4，a），（b，6），则a+b=（ ）
有理数a、b、c在数轴上的位置如图所示，化简|a+c|+|b+c|-|b-a|．