题目内容
3.先化简,再求值:($\frac{x+1}{x+y}$-$\frac{1-x}{x+y}$)÷$\frac{2x}{{x}^{2}-{y}^{2}}$,其中x=1+$\sqrt{3}$,y=$\sqrt{27}$-2.分析 可先把分式化简,再把x,y的值代入计算求值.
解答 解:原式=$\frac{x+1-1+x}{x+y}×\frac{(x-y)(x+y)}{2x}$
=x-y
把x=1+$\sqrt{3}$,y=$\sqrt{27}$-2代入x-y=$1+\sqrt{3}-3\sqrt{3}+2=3-2\sqrt{3}$.
点评 此题考查分式的混合运算,关键是先把分式化简.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.下列说法中正确的是( )
| A. | -a表示负数 | |
| B. | 多项式-3a2b+7a2b2-2ab+1是四次四项式 | |
| C. | 单项式-$\frac{2x{y}^{2}}{9}$的系数为-2 | |
| D. | 若|x|=-x,则x<0 |


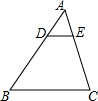 如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,BC=12,则DE的长是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,BC=12,则DE的长是( )