题目内容
5.如图所示,将△ABC沿着DE翻折,点B与点B′对应.图(1)中点B′在∠ABC内部,图(2)中点B′在∠ABC外部,请分别写出∠1、∠2与∠B的数量关系,并说明理由.
分析 ①根据折叠性质得出∠BED=∠B′ED,∠BDE=∠B′DE,根据三角形内角和定理得出∠BED+∠BDE=180°-∠B,代入∠1+∠2=180°+180°-2(∠BED+∠BDE)求出即可;
②由图形翻折变换的性质可得到∠B=∠B′,再根据∠2=∠EB′B+∠EBB′即可求出答案.
解答 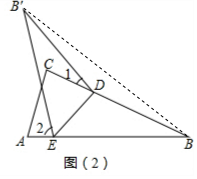 解:①如图(1),2∠B=∠1+∠2,
解:①如图(1),2∠B=∠1+∠2,
理由是:∵延DE折叠B和B′重合,
∴∠BED=∠B′ED,∠BDE=∠B′DE,
∵∠BED+∠BDE=180°-∠B,∠1+∠2=180°+180°-2(∠BED+∠BDE),
∴∠1+∠2=360°-2(180°-∠B)=2∠B;
如图(2)由图形翻折变换的性质可知,∠B=∠B′,
连接BB′,
则∠2=∠EB′B+∠EBB′
=∠DB′E+∠DB′B+∠DBE+∠B′BD,
=2∠B+∠DB′B+∠B′BD
=2∠B+∠1即∠2-∠1=2∠B.
点评 此题考查了折叠的性质,三角形外角性质,三角形内角和定理的应用,主要考查学生运用定理进行推理和计算的能力.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
20.二次函数y=-x2-2x+1的二次项系数是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
10. 一次函数y=kx+b(k≠0)的图象如图所示,当x>2时,y的取值范围是( )
一次函数y=kx+b(k≠0)的图象如图所示,当x>2时,y的取值范围是( )
 一次函数y=kx+b(k≠0)的图象如图所示,当x>2时,y的取值范围是( )
一次函数y=kx+b(k≠0)的图象如图所示,当x>2时,y的取值范围是( )| A. | y<0 | B. | y>0 | C. | y<3 | D. | y>3 |
14.观察下列等式:a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$,a2=$\frac{4}{2×3×{2}^{3}}$=$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$,a3=$\frac{5}{3×4×{2}^{4}}$=$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$,a4=$\frac{6}{4×5×{2}^{5}}$=$\frac{1}{4×{2}^{4}}$-$\frac{1}{5×{2}^{5}}$,…,按以上规律写出了a5、a6、a7、…、a20,则a1+a2+a3+…+a20=( )
| A. | $\frac{1}{2}$-$\frac{1}{20×{2}^{20}}$ | B. | $\frac{1}{19×{2}^{19}}$-$\frac{1}{20×{2}^{20}}$ | ||
| C. | $\frac{1}{20}$-$\frac{1}{21×{2}^{21}}$ | D. | $\frac{1}{2}$-$\frac{1}{21×{2}^{21}}$ |
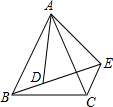 如图,已知AB=AC,AD=AE,∠BAC=∠DAE=50°,B、D、E在同一直线上,则∠BEC的度数为50°.
如图,已知AB=AC,AD=AE,∠BAC=∠DAE=50°,B、D、E在同一直线上,则∠BEC的度数为50°. 如图,BC∥ED,BD、CE相交于点A,且DE=4,BC=8.
如图,BC∥ED,BD、CE相交于点A,且DE=4,BC=8. 集团对应聘者甲、乙、丙进行面试,并从专业知识、工作经验、仪表形象三方面给应聘者打分,每一方面满分20分,最后的打分制成条形统计图(如图).
集团对应聘者甲、乙、丙进行面试,并从专业知识、工作经验、仪表形象三方面给应聘者打分,每一方面满分20分,最后的打分制成条形统计图(如图).