题目内容
15.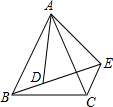 如图,已知AB=AC,AD=AE,∠BAC=∠DAE=50°,B、D、E在同一直线上,则∠BEC的度数为50°.
如图,已知AB=AC,AD=AE,∠BAC=∠DAE=50°,B、D、E在同一直线上,则∠BEC的度数为50°.
分析 由条件可证明△ABD≌△ACE,可知∠ABD=∠ACE,在△ADE中可求得∠ADE,利用外角的性质可求得∠EAC+∠ACE,在△ACE中利用三角形内角和可求得∠BEC.
解答 解:
∵∠BAC=∠DAE=50°,
∴∠BAD=∠CAE,
在△ABD和△ACE中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$
∴△ABD≌△ACE(SAS),
∴∠BAD=∠CAE,∠ABD=∠ACE,
∵AD=AE,∠DAE=50°,
∴∠ADE=∠AED=65°,
∵∠BAD+∠ABD=∠ADE,
∴∠CAE+∠ACE=∠ADE=65°,
在△ACE中,∠BEC=180°-∠AEC-(∠CAE+∠ACE)=180°-65°-65°=50°,
故答案为:50°.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应角相等、对应边相等)是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,AB∥CD,E为AD边的中点,再过点E作EF∥AB,交BC于F
如图,AB∥CD,E为AD边的中点,再过点E作EF∥AB,交BC于F 如图,DA=DC,∠B=72°,∠C=36°,则∠BAD=36度.
如图,DA=DC,∠B=72°,∠C=36°,则∠BAD=36度. 如图,已知△ABC,试用直尺和圆规作出△ABC的角平分线CE、高AD.(尺规作图,保留痕迹,不写作法)
如图,已知△ABC,试用直尺和圆规作出△ABC的角平分线CE、高AD.(尺规作图,保留痕迹,不写作法)