题目内容
11.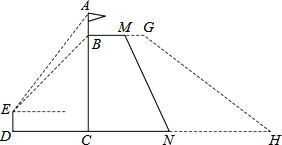 如图,我国某边防哨所树立了“祖国在我心中”建筑物,它的横截面为四边形BCNM,其中BC⊥CN,BM∥CN,建筑物顶上有一旗杆AB,士兵小明站在D处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,已知旗杆AB=2.8米,DE=1.8米.
如图,我国某边防哨所树立了“祖国在我心中”建筑物,它的横截面为四边形BCNM,其中BC⊥CN,BM∥CN,建筑物顶上有一旗杆AB,士兵小明站在D处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,已知旗杆AB=2.8米,DE=1.8米.(参考数据:sin52°≈0.788,tan52°≈1.280)
(1)求建筑物的高度BC;
(2)建筑物长50米,背风坡MN的坡度i=1:0.5,为提高建筑物抗风能力,士兵们在背风坡填筑土石方加固,加固后建筑物顶部加宽4.2米,背风坡GH的坡度为i=1:1.5,施工10天后,边防居民为士兵支援的机械设备终于到达,这样工作效率提高到了原来的2倍,结果比原计划提前20天完成加固任务,士兵们原计划平均每天填筑土石方多少立方米?
分析 (1)根据题意得出EF=BF,进而利用tan∠AEF=$\frac{AF}{EF}$即可得出答案;
(2)利用坡比的定义得出QN,QH的长,进而利用梯形面积求法求出总的土方量,进而得出答案.
解答  解:(1)如图所示:过点E作EF⊥BF交BC于点F,设EF=x,
解:(1)如图所示:过点E作EF⊥BF交BC于点F,设EF=x,
则EF=x,则根据题意可得:BF=x,
同理可知tan∠AEF=$\frac{AF}{EF}$=$\frac{2.8+x}{x}$≈1.28,
解得:x=10,
即BC=10+1.8=11.8(m).
答:建筑物的高度BC为11.8m;
(2)如图所示:过点M,G分别作MQ、GP垂直于CN,交CN于点Q、P,
根据题意可得:PH=11.8×1.5=17.7(m),QN=5.9(m),
可得:NH=17.7-5.9+4.2=16(m),
故可得加固所需土石方为:$\frac{1}{2}$(MG+NH)×PG=$\frac{1}{2}$×11.8×(4.2+16)×50=5959,
则根据题意可列方程:设原计划每天填筑土石方a立方米,
$\frac{5959}{a}$-20=10+$\frac{5959-10a}{2a}$,
解得:a=119$\frac{9}{50}$,
经检验得:a=119$\frac{9}{50}$是原方程的解且符合题意,
答:士兵们原计划平均每天填筑土石方119$\frac{9}{50}$立方米.
点评 此题考查了解直角三角形的应用,把实际问题转化为解直角三角形问题,再正确得出QH,NH的长是解题关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
1.如果x=1是方程x2+ax+1=0的一个根,那么a的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | -2 |
3.下列计算中,正确的是( )
| A. | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B. | $\sqrt{8}×\sqrt{2}=4$ | C. | $2+\sqrt{3}=2\sqrt{3}$ | D. | $\frac{{\sqrt{10}}}{2}=\sqrt{5}$ |
 直线AB、CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,求∠EOB的度数.
直线AB、CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,求∠EOB的度数.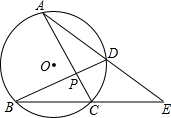 如图,AC与BD交于P,AD、BC延长交于点E,∠AEC=37°,∠CAE=31°,则∠APB的度数为99°.
如图,AC与BD交于P,AD、BC延长交于点E,∠AEC=37°,∠CAE=31°,则∠APB的度数为99°.