题目内容
关于x的二次函数y=kx2+kx+1-k(k≠0)与一次函数的图象交于点A(1,1+k),B(0,1-k)
(1)求一次函数表达式(含有常数k);
(2)猜测对任意实数k(k≠0),二次函数图象都具有的特征,并说明理由(写两条);
(3)要使一次函数与二次函数都是y随x的增大而减小,求k满足的条件以及x的取值范围.
(1)求一次函数表达式(含有常数k);
(2)猜测对任意实数k(k≠0),二次函数图象都具有的特征,并说明理由(写两条);
(3)要使一次函数与二次函数都是y随x的增大而减小,求k满足的条件以及x的取值范围.
考点:二次函数的性质,待定系数法求一次函数解析式
专题:
分析:(1)根据待定系数法即可求得一次函数的表达式.
(2)猜想:不论k取何值,函数y=kx2+kx+1-k(k≠0的图象的对称轴x=-
,必过定点(
,1),(
,1).由对称轴方程公式得x=-
,由解析式变形,得y=k(x2+x-1)+1,可知当x2+x-1=0,即x=
或
时,函数值与k的取值无关,此时y=1,可得定点坐标;
(3)根据一次函数和二次函数的性质即可得出一次函数与二次函数都是y随x的增大而减小时,k满足的条件以及x的取值范围.
(2)猜想:不论k取何值,函数y=kx2+kx+1-k(k≠0的图象的对称轴x=-
| 1 |
| 2 |
-1+
| ||
| 2 |
-1-
| ||
| 2 |
| 1 |
| 2 |
-1+
| ||
| 2 |
-1-
| ||
| 2 |
(3)根据一次函数和二次函数的性质即可得出一次函数与二次函数都是y随x的增大而减小时,k满足的条件以及x的取值范围.
解答:
解:(1)设直线的解析式为y=ax+b,
∵一次函数的图象经过点A(1,1+k),B(0,1-k),
∴
,解得
,
∴一次函数表达式为y=2k+1-k.
(2)不论k取何值,函数y=kx2+kx+1-k(k≠0的图象的对称轴x=-
,必过定点(
,1),(
,1).
证明如下:
将x=
时代入函数中解出y=1.
所以函数的图象必过定点(
,1),(
,1).
对称轴x=-
=-
=-
.
所以不论k取何值,函数y=kx2+kx+1-k(k≠0的图象的对称轴是定值.
(3)由直线y=2k+1-k可知当k<0时,y随x的增大而减小,对于二次函数y=kx2+kx+1-k(k≠0)的图象开口向下,在对称轴的右侧,y随x的增大而减小,
∵函数y=kx2+kx+1-k(k≠0的图象的对称轴x=-
,
∴当k<0,且x>-
时一次函数与二次函数都是y随x的增大而减小.
∵一次函数的图象经过点A(1,1+k),B(0,1-k),
∴
|
|
∴一次函数表达式为y=2k+1-k.
(2)不论k取何值,函数y=kx2+kx+1-k(k≠0的图象的对称轴x=-
| 1 |
| 2 |
-1+
| ||
| 2 |
-1-
| ||
| 2 |
证明如下:
将x=
-1±
| ||
| 2 |
所以函数的图象必过定点(
-1+
| ||
| 2 |
-1-
| ||
| 2 |
对称轴x=-
| b |
| 2a |
| k |
| 2k |
| 1 |
| 2 |
所以不论k取何值,函数y=kx2+kx+1-k(k≠0的图象的对称轴是定值.
(3)由直线y=2k+1-k可知当k<0时,y随x的增大而减小,对于二次函数y=kx2+kx+1-k(k≠0)的图象开口向下,在对称轴的右侧,y随x的增大而减小,
∵函数y=kx2+kx+1-k(k≠0的图象的对称轴x=-
| 1 |
| 2 |
∴当k<0,且x>-
| 1 |
| 2 |
点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法、二次函数的增减性等知识点.主要考查学生数形结合的数学思想方法.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
下列说法中正确的是( )
| A、所有连接两点的线中,直线最短 |
| B、连接两点之间的线段叫做两点间的距离 |
| C、如果点P是线段AB的中点,那么AP=BP |
| D、如果AP=BP,那么点P是线段AB的中点 |
 AD是△ABC的高,下列能使△ABD≌ACD的条件是( )
AD是△ABC的高,下列能使△ABD≌ACD的条件是( )| A、BD=AC |
| B、∠B=45° |
| C、∠BAC=90° |
| D、AB=AC |
正方形具有而菱形不一定具有的性质是( )
| A、四条边相等 |
| B、对角线互相垂直平分 |
| C、对角线平分一组对角 |
| D、对角线相等 |
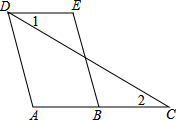 已知:如图,AD∥BE,∠1=∠2,∠A=120°,求∠E的度数.
已知:如图,AD∥BE,∠1=∠2,∠A=120°,求∠E的度数. 如图,直线AB∥x轴,与抛物线y=ax2+bx+c交于点A(-2,-
如图,直线AB∥x轴,与抛物线y=ax2+bx+c交于点A(-2,-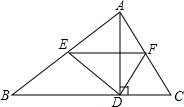 如图,在△ABC中,AD是高.
如图,在△ABC中,AD是高.