Question

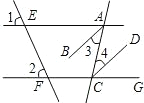
如图，直线AE、CF分别被直线EF、AC所截，已知，∠1=∠2，AB平分∠EAC，CD平分∠ACG．将下列证明AB∥CD的过程及理由填写完整．

证明：∵ ∠1=∠2 （ 已知 ）
∴  AE∥     （                                     ）
∴ ∠EAC =∠        ，（                               ）
而AB平分∠EAC，CD平分∠ACG（ 已知 ）
∴ ∠     = ∠EAC，∠4= ∠         （ 角平分线的定义 ）
∴ ∠    =∠4（等量代换）
∴ AB∥CD（                                      ）．

Answer 1

∵ ∠1=∠2 （ 已知 ）
∴   AE∥PG（同位角相等，两直线平行 ）
∴ ∠EAC =∠ACG  ，（   两直线平行，内错角相等 ）
而 AB平分∠EAC，CD平分∠ACG（ 已知 ）
∴ ∠ 3 = ∠EAC，∠4= ∠  ACG （ 角平分线的定义 ）
∴ ∠  3  =∠4（等量代换）
∴ AB∥CD（ 内错角相等，两直线平行）·

解析试题分析：根据平行线的判定和性质进行填空即可．
考点：平行线的判定与性质；角平分线的定义．
点评：本题解题的关键是理清角之间的关系．