题目内容
设直线l1:y=x-1交x轴于点A,交y轴于点D,直线l2:y=-
x+
交y轴于点B,且l1与l2交于点C,求△ABC的面积S.
| 1 |
| 2 |
| 7 |
| 2 |
考点:两条直线相交或平行问题
专题:
分析:直接利用直线l1与直线l2的解析式组成方程组即可求出点C坐标;利用两条直线的解析式可以分别求出A、B两点的坐标,结合图形即可求出△ABC的面积.
解答: 解:依题意得
解:依题意得
,
解得
,
∴C(9,8);
令y=0分别代入直线l1、l2解析式得,
x=1,或x=-7,
∴A(1,0),B(-7,0),
∴BC=1+7=8,
∴S△ABC=
AB•|yC|=
×8×8=32;
 解:依题意得
解:依题意得
|
解得
|
∴C(9,8);
令y=0分别代入直线l1、l2解析式得,
x=1,或x=-7,
∴A(1,0),B(-7,0),
∴BC=1+7=8,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了利用直线的解析式求直线交点坐标,和直线坐标轴相关的三角形的面积计算等知识,综合性比较强,对学生的要求比较高.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
下列运算中,正确的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知抛物线y=x2-x-2与x轴的一个交点为(m,0),则代数式m2-m+2008的值为( )
| A、2007 | B、2008 |
| C、2009 | D、2010 |
 如图,已知AD是△ABC的中线,且AE:EB=1:6,射线CF交AD于点F,则AF:FD=
如图,已知AD是△ABC的中线,且AE:EB=1:6,射线CF交AD于点F,则AF:FD=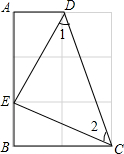 如图,四边形ABCD中,如果∠A=∠B=90°,∠1=∠2=45°,使A,E,B在同一直线上,连接CD,并且AD=BE.
如图,四边形ABCD中,如果∠A=∠B=90°,∠1=∠2=45°,使A,E,B在同一直线上,连接CD,并且AD=BE.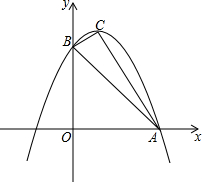 如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.
如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.