题目内容
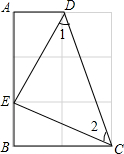 如图,四边形ABCD中,如果∠A=∠B=90°,∠1=∠2=45°,使A,E,B在同一直线上,连接CD,并且AD=BE.
如图,四边形ABCD中,如果∠A=∠B=90°,∠1=∠2=45°,使A,E,B在同一直线上,连接CD,并且AD=BE.(1)求证:Rt△ADE≌Rt△BEC;
(2)若AD=3,AB=7,请求出△ECD的面积;
(3)若P为CD的中点,连接PA、PB.试判断△APB的形状,并证明之.
考点:全等三角形的判定与性质
专题:
分析:(1)易证∠ADE=∠BEC和DE=CE,即可证明RT△ADE≌RT△BEC,即可解题;
(2)由(1)结论可得AD=BE,即可求得AE的长,根据勾股定理可求得DE的长,即可解题;
(3)连结PE,易证∠PEB=∠PDA和PE=PD,即可证明△BEP≌△ADP,可得PA=PB,∠APD=∠BPE,根据∠APD+∠APE=90°,即可求得∠APB=90°,即可判定△APB为等腰直角三角形.
(2)由(1)结论可得AD=BE,即可求得AE的长,根据勾股定理可求得DE的长,即可解题;
(3)连结PE,易证∠PEB=∠PDA和PE=PD,即可证明△BEP≌△ADP,可得PA=PB,∠APD=∠BPE,根据∠APD+∠APE=90°,即可求得∠APB=90°,即可判定△APB为等腰直角三角形.
解答:(1)证明:∵∠AED+∠ADE=90°,∠AED+∠BEC=90°,
∴∠ADE=∠BEC,
∵∠1=∠2,
∴DE=CE,
在△ADE和△BEC中,
,
∴RT△ADE≌RT△BEC(AAS),
(2)解:∵RT△ADE≌RT△BEC,
∴AD=BE,
∵AD=3,AB=7,
∴AE=4.
在Rt△AED中,由勾股定理,得DE=5,
∴EC=5,
∴S△CED=
×5×5=12.5;
(3)证明:△APB为等腰直角三角形,
理由:连结PE,
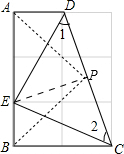
∵P是CD的中点,
∴PD=PC=
CD.
∵ED=EC,∠DEC=90°,
∴∠CEP=
∠DEC,∠EPD=90°,PE=
CD.
∴∠CEP=45°.PE=PD.
∴∠CEP=∠EDC.
∴∠CEP+∠BEC=∠EDC+∠ADE,
∴∠PEB=∠PDA.
在△BEP和△ADP中,
,
∴△BEP≌△ADP(SAS),
∴PA=PB,∠APD=∠BPE,
∵∠APD+∠APE=90°,
∴∠BPE+∠APE=90°,
∴∠APB=90°.
∵PA=PB,
∴△APB为等腰直角三角形.
∴∠ADE=∠BEC,
∵∠1=∠2,
∴DE=CE,
在△ADE和△BEC中,
|
∴RT△ADE≌RT△BEC(AAS),
(2)解:∵RT△ADE≌RT△BEC,
∴AD=BE,
∵AD=3,AB=7,
∴AE=4.
在Rt△AED中,由勾股定理,得DE=5,
∴EC=5,
∴S△CED=
| 1 |
| 2 |
(3)证明:△APB为等腰直角三角形,
理由:连结PE,

∵P是CD的中点,
∴PD=PC=
| 1 |
| 2 |
∵ED=EC,∠DEC=90°,
∴∠CEP=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CEP=45°.PE=PD.
∴∠CEP=∠EDC.
∴∠CEP+∠BEC=∠EDC+∠ADE,
∴∠PEB=∠PDA.
在△BEP和△ADP中,
|
∴△BEP≌△ADP(SAS),
∴PA=PB,∠APD=∠BPE,
∵∠APD+∠APE=90°,
∴∠BPE+∠APE=90°,
∴∠APB=90°.
∵PA=PB,
∴△APB为等腰直角三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△BEP≌△ADP是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知⊙O的弦CD⊥直径AB,垂足为P,且AP=3,AB=30,那么CD等于( )
| A、9 | ||
B、3
| ||
| C、18 | ||
D、6
|
 如图,在菱形ABCD中,∠A=135°,AB=
如图,在菱形ABCD中,∠A=135°,AB=
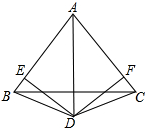 如图,已知BD=CD,∠ABD=∠ACD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.
如图,已知BD=CD,∠ABD=∠ACD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF. 已知点C为∠AOB内一点,OM,ON分别平分∠AOC和∠BOC,则∠MON=
已知点C为∠AOB内一点,OM,ON分别平分∠AOC和∠BOC,则∠MON= 矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0)、C(O,3),直线y=
矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0)、C(O,3),直线y=