题目内容
如图，已知AD是△ABC的中线，且AE：EB=1：6，射线CF交AD于点F，则AF：FD=考点：平行线分线段成比例,三角形中位线定理
专题：计算题
分析：作DG∥CE交AB于G，如图，根据平行线分线段成比例定理，由DG∥CE得到
=
，而BD=DC，则BG=GE，于是由AE：EB=1：6得到AE：EG=1：3，然后利用EF∥DG，可得AF：FD=AE：EG=1：3．
| BG |
| GE |
| BD |
| DC |
解答：解：作DG∥CE交AB于G，如图，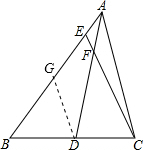
∵DG∥CE，
∴
=
，
∵AD是△ABC的中线，
∴BD=DC，
∴BG=GE，
∵AE：EB=1：6，
∴AE：EG=1：3，
∵EF∥DG，
∴AF：FD=AE：EG=1：3．
故答案为1：3．
∵DG∥CE，
∴
| BG |
| GE |
| BD |
| DC |
∵AD是△ABC的中线，
∴BD=DC，
∴BG=GE，
∵AE：EB=1：6，
∴AE：EG=1：3，
∵EF∥DG，
∴AF：FD=AE：EG=1：3．
故答案为1：3．
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
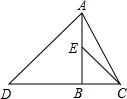如图，AB⊥CD于B，△ABD与△BCE都是等腰直角三角形，若BD=12，AC=13，则△ACE的面积为（ ）| A、30 | B、35 |
| C、17.5 | D、15 |
已知⊙O的弦CD⊥直径AB，垂足为P，且AP=3，AB=30，那么CD等于（ ）
| A、9 | ||
B、3
| ||
| C、18 | ||
D、6
|
如图，在菱形ABCD中，∠A=135°，AB=
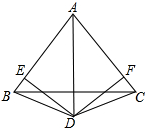如图，已知BD=CD，∠ABD=∠ACD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．
如图，已知大正方形和小正方形的边长分别为a、b