题目内容
把抛物线y=（x+d）2+h向左平移4个单位，再向上平移2个单位，得到抛物线y=x2，求函数的解析式．
考点：二次函数图象与几何变换
专题：几何变换
分析：利用逆向思维的形式解决问题：先得到抛物线y=x2的顶点坐标为（0，0），再根据点的平移规律把点（0，0）向右平移4个单位，再向下平移2个单位得到点的坐标为（-4，-2），然后根据顶点式写出抛物线解析式．
解答：解：抛物线y=x2的顶点坐标为（0，0），把点（0，0）向右平移4个单位，再向下平移2个单位得到点的坐标为（-4，-2），
所以原抛物线解析式为y=（x+4）2-2．
所以原抛物线解析式为y=（x+4）2-2．
点评：本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
如图，直线y=x+1与y轴交于点A，与反比例函数y=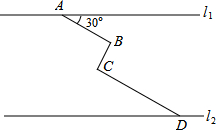
如图，在同一平面内，两条平行高速公路l1和l2间有一条“Z”型道路连通，其中AB段与高速公路l1成30°角，长为20km； BC段与AB、CD段都垂直，BC段长为10km，CD段长为30km．则两条高速公路l1和l2间的距离为
如图，A、B是双曲线y=