题目内容
已知,在直角坐标平面内有点A(3,0)、B(0,6),求:一个正比例函数的解析式,使它的图象将△AOB的面积分成1:2两个部分.
考点:一次函数的性质
专题:
分析:设所求直线y=kx与AB交于点C,当直线OC将△AOB的面积分成1:2两个部分时,分两种情况进行讨论:①S△AOC=
S△AOB;②S△BOC=
S△AOB;利用面积之间的关系分别求出C点坐标,进而求出直线OC的解析式.
| 1 |
| 3 |
| 1 |
| 3 |
解答: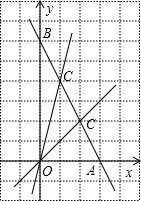 解:∵A(3,0)、B(0,6),
解:∵A(3,0)、B(0,6),
∴直线AB的解析式为y=-2x+6.
设所求直线y=kx与AB交于点C(x,y),当直线OC将△AOB的面积分成1:2两个部分时,分两种情况进行讨论:
①如果S△AOC=
S△AOB,那么
×3y=
×
×3×6,
解得y=2,
将y=2代入y=-2x+6,得2=-2x+6,
解得x=2,
所以C(2,2),
此时所求直线的解析式为y=x;
②如果S△BOC=
S△AOB,那么
×6x=
×
×3×6,
解得x=1,
将x=1代入y=-2x+6,得y=-2×1+6=4,
所以C(1,4),
此时所求直线的解析式为y=4x;
综上所述,所求正比例函数的解析式为y=x或y=4x.
 解:∵A(3,0)、B(0,6),
解:∵A(3,0)、B(0,6),∴直线AB的解析式为y=-2x+6.
设所求直线y=kx与AB交于点C(x,y),当直线OC将△AOB的面积分成1:2两个部分时,分两种情况进行讨论:
①如果S△AOC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
解得y=2,
将y=2代入y=-2x+6,得2=-2x+6,
解得x=2,
所以C(2,2),
此时所求直线的解析式为y=x;
②如果S△BOC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
解得x=1,
将x=1代入y=-2x+6,得y=-2×1+6=4,
所以C(1,4),
此时所求直线的解析式为y=4x;
综上所述,所求正比例函数的解析式为y=x或y=4x.
点评:本题考查了一次函数的性质,运用待定系数法求一次函数的解析式,三角形的面积,难度适中.利用数形结合与分类讨论是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
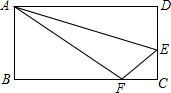 如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE,AB=CD=6,AD=BC=10,试求EC的长度.
如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE,AB=CD=6,AD=BC=10,试求EC的长度.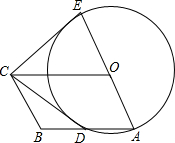 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,