题目内容
百货商店服装柜在销售中发现:某童装每天可卖20件,每件盈利40元,为迎接“六一”儿童节,商场决定采取适当降价措施,扩大销售量,增加盈利,减少库存,经市场调查发现:每件童装降价1元,每天可多卖2件,要想平均每天获利1200元,那么每件童装应降价多少元?要使每天盈利最多,每件应降价多少元?
考点:一元二次方程的应用,二次函数的应用
专题:
分析:(1)利用童装平均每天售出的件数×每件盈利=每天销售这种童装利润列出方程解答即可;
(2)设每天销售这种童装利润为y,利用上面的关系列出函数,利用配方法解决问题.
(2)设每天销售这种童装利润为y,利用上面的关系列出函数,利用配方法解决问题.
解答:解:(1)设每件童装应降价x元,根据题意列方程得,
(40-x)(20+2x)=1200,
解得x1=20,x2=10(因为尽快减少库存,不合题意,舍去).
答:每件童装降价20元;
(2)设每天销售这种童装利润为y,
则y=(40-x)(20+
×5)=-2x2+60x+800=-2(x-15)2+1250,
答:当每件童装降价15元时,能获最大利润1250元.
(40-x)(20+2x)=1200,
解得x1=20,x2=10(因为尽快减少库存,不合题意,舍去).
答:每件童装降价20元;
(2)设每天销售这种童装利润为y,
则y=(40-x)(20+
| x |
| 2.5 |
答:当每件童装降价15元时,能获最大利润1250元.
点评:此题主要考查了一元二次方程的实际应用和二次函数实际中的应用,此题找到关键描述语,找到等量关系准确的列出方程或函数关系式是解决问题的关键.最后要注意判断所求的解是否符合题意,舍去不合题意的解.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
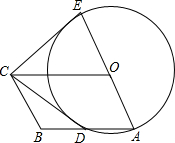 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线, 如图,四边形ABCD是平行四边形,∠ADC=125°,∠CAD=21°,求∠ABC、∠CAB的度数.
如图,四边形ABCD是平行四边形,∠ADC=125°,∠CAD=21°,求∠ABC、∠CAB的度数.