题目内容
如图，OD、OE分别是∠AOC、∠BOC的平分线，∠EOD=60°，求∠AOB的度数．
解：∵OD是∠AOC的平分线，
∴∠AOC=2∠DOC，
∵OE是∠BOC的平分线，
∴∠BOC=2∠EOC，
∴∠AOB=2∠DOE，
∵∠EOD=60°，
∴∠AOB=120°．
故答案为120°．
分析：根据角平分线的概念以及角的和的关系，找到∠AOB和∠EOD之间的关系．
点评：此题中注意发现：∠AOB=2∠EOD．重点是能够用几何式子根据角平分线的概念表示角之间的倍分关系．
∴∠AOC=2∠DOC，
∵OE是∠BOC的平分线，
∴∠BOC=2∠EOC，
∴∠AOB=2∠DOE，
∵∠EOD=60°，
∴∠AOB=120°．
故答案为120°．
分析：根据角平分线的概念以及角的和的关系，找到∠AOB和∠EOD之间的关系．
点评：此题中注意发现：∠AOB=2∠EOD．重点是能够用几何式子根据角平分线的概念表示角之间的倍分关系．
练习册系列答案
相关题目
如图，∠AOB=60°，OD、OE分别平分∠BOC、∠AOC，那么∠EOD=
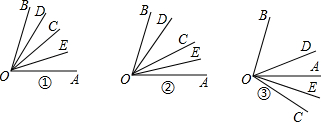
如图，已知∠AOB=2∠BOC，又OD，OE分别为∠AOB和∠BOC的平分线，若∠DOE=66°．
