题目内容
14.解下面的不等式或不等式组,并在数轴上表示出解集.(1)$\frac{1}{4}$x-6≤3-$\frac{1}{5}$x
(2)$\left\{\begin{array}{l}{4(x+1)+3>x}\\{\frac{x-4}{2}≤\frac{x-5}{3}}\end{array}\right.$.
分析 (1)首先移项,把含x的项移到不等式左边,常数项移到右边,然后再合并同类项,最后把x的系数化为1即可;
(2)首先分别解出两个不等式的解集,再根据解集的规律:大小小大中间找确定不等式组的解集即可.
解答 解:(1)移项得:$\frac{1}{4}$x+$\frac{1}{5}$x≤6+3,
合并同类项得:$\frac{9}{20}$x≤9,
把x的系数化为1得:x≤20,
在数轴上表示为: ;
;
(2)$\left\{\begin{array}{l}{4(x+1)+3>x①}\\{\frac{x-4}{2}≤\frac{x-5}{3}②}\end{array}\right.$,
由①得:x>-$\frac{7}{3}$,
由②得:x≤2,
在数轴上表示: ,
,
不等式组的解集为:-$\frac{7}{3}$<x≤2.
点评 此题主要考查了解一元一次不等式(组)的解法,以及在数轴上表示解集,在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
相关题目
 如图所示,电镀螺杆呈现出了两个几何体的组合,则这个两个几何体分别是圆柱、六棱柱.
如图所示,电镀螺杆呈现出了两个几何体的组合,则这个两个几何体分别是圆柱、六棱柱.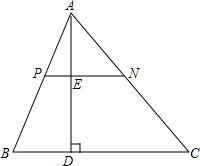 已知:如图所示,PN∥BC,AD⊥BC交PN于点E,交BC于点D.
已知:如图所示,PN∥BC,AD⊥BC交PN于点E,交BC于点D.
 如图,AB∥CD,点E在BC上,∠BED=68°,∠D=38°,则∠B的度数为30°.
如图,AB∥CD,点E在BC上,∠BED=68°,∠D=38°,则∠B的度数为30°.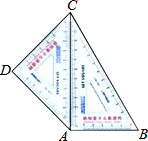 如图,学生用三角板中,等腰直角三角形三角板的斜边靠在另一个含60°角的三角形板的对边上恰好完全重合,拼成一个四边形ABCD.若60°所对的直角边长为12cm,求拼成四边形ABCD的面积.
如图,学生用三角板中,等腰直角三角形三角板的斜边靠在另一个含60°角的三角形板的对边上恰好完全重合,拼成一个四边形ABCD.若60°所对的直角边长为12cm,求拼成四边形ABCD的面积.