题目内容
7.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆金鱼的比赛,如图所示.
按以上的规律,第n个图形需要的火柴棒m关于n的函数表达式为( )
| A. | m=8n | B. | m=8+6n | C. | m=4+4n | D. | m=2+6n |
分析 观察给出的3个例图,注意火柴棒根数的变化是图②的火柴棒比图①的多6根,图③的火柴棒比图②的多6根,据此找出规律即可解答.
解答 解:由图形可知:
第一个金鱼需用火柴棒的根数为:2+6=8;
第二个金鱼需用火柴棒的根数为:2+2×6=14;
第三个金鱼需用火柴棒的根数为:2+3×6=20;
…;
第n个金鱼需用火柴棒的根数为:2+n×6=2+6n.
所以第n个图形需要的火柴棒m关于n的函数表达式为:m=2+6n.
故选:D.
点评 本题考查列代数式,本题的解答体现了由特殊到一般的数学方法(归纳法),先观察特例,找到火柴棒根数的变化规律,然后猜想第n条小鱼所需要的火柴棒的根数.

练习册系列答案
相关题目
10.某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
| 类别/单价 | 成本价 | 销售价(元/箱) |
| 甲 | 24 | 36 |
| 乙 | 33 | 48 |
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
7.射击训练中,甲、乙、丙、丁四人每人射击10次,平均环数均为8.7环,方差分别为S甲2=0.51,S乙2=0.41、S丙2=0.62、S丁2=0.45,则四人中成绩最稳定的是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
16. 如图,在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )
如图,在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )
 如图,在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )
如图,在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )| A. | 1 | B. | $\sqrt{5}$ | C. | $\sqrt{13}$ | D. | 5 |
 已知甲、乙、丙三个村计划修建一个贮物库,使三个村到贮物库的距离一样,请你帮这三个村设计贮物库的具体位置.
已知甲、乙、丙三个村计划修建一个贮物库,使三个村到贮物库的距离一样,请你帮这三个村设计贮物库的具体位置.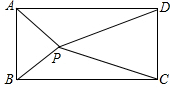 如图,四边形ABCD是长方形,点P是长方形内的任意一点,求证:PA2+PC2=PB2+PD2.
如图,四边形ABCD是长方形,点P是长方形内的任意一点,求证:PA2+PC2=PB2+PD2.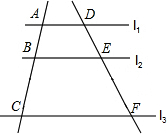 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F.设AB=3,BC=5,DE=4,则EF=$\frac{20}{3}$.
如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F.设AB=3,BC=5,DE=4,则EF=$\frac{20}{3}$.