题目内容
1. 如图,△ABC中,BE平分∠ABC,BD=DE,AB=$\frac{5}{2}$cm,BD=2cm,则BC=10cm.
如图,△ABC中,BE平分∠ABC,BD=DE,AB=$\frac{5}{2}$cm,BD=2cm,则BC=10cm.
分析 先证明DE∥BC,再根据平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例得到$\frac{DE}{BC}$=$\frac{AD}{AB}$,然后利用比例性质求BC.
解答 解:∵BD=BE,
∴∠DBE=∠DEB,
∵BE平分∠ABC,
∴∠DBE=∠CBE,
∴∠CBE=∠DEB,
∴DE∥BC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$,
而DE=BD=2,AD=AB-BD=$\frac{1}{2}$,
∴$\frac{2}{BC}$=$\frac{\frac{1}{2}}{\frac{5}{2}}$,
∴BC=10(cm).
故答案为10.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例;平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.

练习册系列答案
相关题目
13.已知函数y=kx+b,其x与y的部分对应值如下表,解关于x的不等式kx+b<0.
| x | -1 | 0 | 1 | 2 |
| y | 4 | 2 | 0 | -2 |
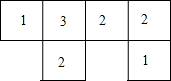 如图从上面看由11个小立方块摆成的模型所得的平面图,小正方形中的数字表示该位置小正方块的个数,请画出这个模型从正面看,从左面看以及从左面看所得到的图形.
如图从上面看由11个小立方块摆成的模型所得的平面图,小正方形中的数字表示该位置小正方块的个数,请画出这个模型从正面看,从左面看以及从左面看所得到的图形.