题目内容
11.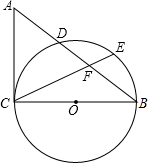 如图,△ABC中,以BC为直径的半圆O交AB于点D.点E为$\widehat{BD}$的中点,CE与AB交于点F,且AF=AC.
如图,△ABC中,以BC为直径的半圆O交AB于点D.点E为$\widehat{BD}$的中点,CE与AB交于点F,且AF=AC.(1)求证:AC是⊙O的切线;
(2)若BC=8,BF=4,求DF的长.
分析 (1)由圆周角定理得出∠BEC=90°,∠EBF=∠BCE,得出∠EBF+∠EFB=90°,再证出∠EFB=∠ACF,求出∠ACF+∠BCE=90°,即可得出结论;
(2)连接CD,作FM⊥BC于M.设AC=AF=x,在Rt△ABC中,利用勾股定理求出x,再证明Rt△FCD≌Rt△FCM,可得CM=CD=$\frac{24}{5}$,BM=$\frac{16}{5}$,BD=$\frac{32}{5}$,设DF=FM=y,在Rt△FBM中,根据FM2+BM2=FB2,列出方程求出y即可;
解答 (1)证明:连接BE,如图所示: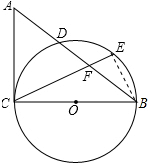 ∵BC为直径,
∵BC为直径,
∴∠BEC=90°,
∴∠EBF+∠EFB=90°,
∵E为弧BD的中点,
∴$\widehat{DE}$=$\widehat{BE}$,
∴∠EBF=∠BCE,
∵AC=AF,
∴∠ACF=∠AFC,
∵∠AFC=∠EFB,
∴∠EFB=∠ACF,
∴∠ACF+∠BCE=90°,
∴OC⊥AC,
∵AC经过⊙O外端点C,
∴AC是⊙O的切线;
(2)解:连接CD,作FM⊥BC于M.设AC=AF=x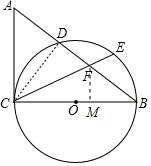
在Rt△ACB中,∵AC2+BC2=AB2,
∴x2+82=(x+4)2,
∴x=6,
∴AC=6,AC=10,
∵BC是直径,
∴∠CDB=90°,即CD⊥AB,
∵$\frac{1}{2}$•AC•BC=$\frac{1}{2}$•AB•CD,
∴CD=$\frac{24}{5}$,
∵$\widehat{DE}$=$\widehat{BE}$,
∴∠FCD=∠FCB,
∵FD⊥DC,FM⊥BC,
∴FD=FM,∵CF=CF,
∴Rt△FCD≌Rt△FCM,
∴CM=CD=$\frac{24}{5}$,BM=$\frac{16}{5}$,BD=$\frac{32}{5}$,设DF=FM=y,
在Rt△FBM中,∵FM2+BM2=FB2,
∴y2+($\frac{16}{5}$)2=($\frac{32}{5}$-y)2,
解得y=$\frac{12}{5}$,
∴DF=$\frac{12}{5}$.
点评 本题考查了切线的判定、圆周角定理、全等三角形的判定与性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.

| A. | 原价减去15元后再打9折 | B. | 原价打9折后再减去15元 | ||
| C. | 原价减去15元后再打1折 | D. | 原价打1折后再减去15元 |
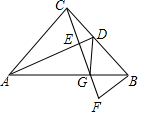 如图,在△ABC中,AC=BC,AC⊥BC,D为BC的中点,CF⊥AD于E,BF∥AC,证明:DG=FG.
如图,在△ABC中,AC=BC,AC⊥BC,D为BC的中点,CF⊥AD于E,BF∥AC,证明:DG=FG.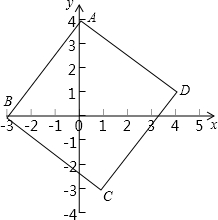 正方形ABCD在平面直角坐标系中的位置如图所示,已知A点的坐标(0,4),B点的坐标(-3,0),求C、D两点的坐标.
正方形ABCD在平面直角坐标系中的位置如图所示,已知A点的坐标(0,4),B点的坐标(-3,0),求C、D两点的坐标.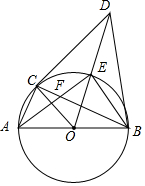 如图,AB为⊙O的直径,BC为⊙O的弦,过O点作OD⊥BC,交⊙O的切线CD于点D,交⊙O于点E,连接AC、AE,且AE与BC交于点F.
如图,AB为⊙O的直径,BC为⊙O的弦,过O点作OD⊥BC,交⊙O的切线CD于点D,交⊙O于点E,连接AC、AE,且AE与BC交于点F.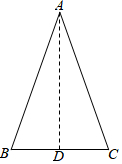 命题:有两个角相等的三角形是等腰三角形(简称“等角对等边”).
命题:有两个角相等的三角形是等腰三角形(简称“等角对等边”).