题目内容
4.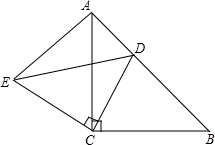 如图,△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,且点D在AB边上,连接AE,
如图,△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,且点D在AB边上,连接AE,(1)求证:△ACE≌△BCD;
(2)求证:DE2=AD2+BD2.
分析 (1)由于△ABC和△DCE都是等腰直角三角形,那么∠B=∠BAC=45°,AC=BC,CE=CD,∠ACB=∠DCE=90°,结合等式性质易证∠1=∠2,那么利用SAS可证△ACD和△BCE.
(2)易求∠EAD=90°,再利用勾股定理可得AE2+AD2=DE2.
解答 证明:∵△ABC和△DCE都是等腰直角三角形,
∴∠B=∠BAC=45°,AC=BC,CE=CD,∠ACB=∠DCE=90°,
∴∠ACB-∠ACE=∠DCE-∠ACE,
即∠ACE=∠BCD,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD,
∴∠CAE=∠B=45°,AE=BD,
∴∠EAD=∠DAC+∠CAE=45°+45°=90°,
∴AE2+AD2=BD2+AD2=DE2.
∴DE2=AD2+BD2
点评 本题考查了全等三角形的判定和性质、等腰直角三角形的性质、勾股定理,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
14.如果□×3a=-3a2b,则“□”内应填的代数式是( )
| A. | -ab | B. | -3ab | C. | a | D. | -3a |
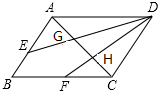 如图所示,在△ABC中,F,E分别为AB,BC的中点,G,H是AC的三等分点,EH,FG的延长线交于点D,连接AD,DC.
如图所示,在△ABC中,F,E分别为AB,BC的中点,G,H是AC的三等分点,EH,FG的延长线交于点D,连接AD,DC.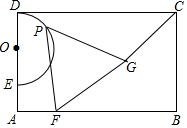 如图,E是矩形ABCD边AD上一点,以DE为直径向矩形内部作半圆O,AB=4$\sqrt{3}$,OD=2,点G在矩形内部,且∠GCB=30°,GC=2$\sqrt{3}$,过半圆弧(含点D,E)上动点P作PF⊥AB于点F.当△PFG是等边三角形时,PF的长是4或6.
如图,E是矩形ABCD边AD上一点,以DE为直径向矩形内部作半圆O,AB=4$\sqrt{3}$,OD=2,点G在矩形内部,且∠GCB=30°,GC=2$\sqrt{3}$,过半圆弧(含点D,E)上动点P作PF⊥AB于点F.当△PFG是等边三角形时,PF的长是4或6.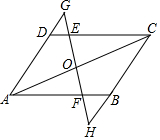 如图.在?ABCD中,点E、F分别在DC、AB上,DE=BF,直线EF分别与AD、CB的延长线相交于点G、H.求证:AC、GH互相平分.
如图.在?ABCD中,点E、F分别在DC、AB上,DE=BF,直线EF分别与AD、CB的延长线相交于点G、H.求证:AC、GH互相平分.