题目内容
11．联通公司手机话费收费有A套餐（月租费15元，通话费每分钟0.1元）和B套餐（月租费0元，通话费每分钟0.15元）两种．设A套餐每月话费为y1（元），B套餐每月话费为y2（元），月通话时间为x分钟．（1）分别表示出y1与x，y2与x的函数关系式．
（2）什么情况下你选择哪种套餐更省钱？
分析 （1）根据A套餐的收费为月租加上话费，B套餐的收费为话费列式即可；
（2）利用方程或不等式即可解决问题；
解答 解：（1）A套餐的收费方式：y1=0.1x+15；
B套餐的收费方式：y2=0.15x；
（2）由0.1x+15=0.15x，得到x=300，
由0.1x+15＜0.15x，得到x＞300，
由0.1x+15＞0.15x，得到x＜300，
答：当月通话时间是300分钟时，A、B两种套餐收费一样；
当月通话时间多于300分钟时，A套餐更省钱．
当月通话时间小于300分钟时，B套餐更省钱．
点评 本题考查了一次函数的应用，是典型的电话收费问题，求出两种收费相同的时间是确定选择不同的缴费方式的关键．
练习册系列答案
相关题目
如图，边长为1的小正方形网格中，⊙O的半径为1，点O及点A、B、C、E都在格点上，则∠AED的正弦值是$\frac{\sqrt{5}}{5}$．
20．
如图，是一个几何体的三视图，根据图中所示数据计算这个几何体的侧面积是（ ）
如图，是一个几何体的三视图，根据图中所示数据计算这个几何体的侧面积是（ ）| A． | π | B． | 2π | C． | 4π | D． | 5π |
如图，将正方形ABCO绕点A顺时针旋转一定角度，得到正方形ADEF，ED交线段OC于点G，ED的延长线交线段BC于点P，连AP、AG．
3．
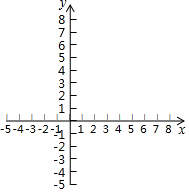数学李老师给学生出了这样一个问题：探究函数y=$\frac{x}{x+1}$的图象与性质，小斌根据学习函数的经验，对函数y=$\frac{x}{x+1}$的图象与性质进行了探究．下面是小斌的探究过程，请您补充完成：
（1）函数y=$\frac{x}{x+1}$的自变量x的取值范围是：x≠-1
（2）列出y与x的几组对应值，请直接写出m的值，m=3．
（3）请在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；
（4）结合函数的图象，写出函数y=$\frac{x}{x+1}$的一条性质．
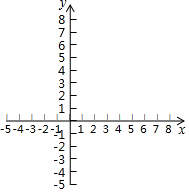数学李老师给学生出了这样一个问题：探究函数y=$\frac{x}{x+1}$的图象与性质，小斌根据学习函数的经验，对函数y=$\frac{x}{x+1}$的图象与性质进行了探究．下面是小斌的探究过程，请您补充完成：（1）函数y=$\frac{x}{x+1}$的自变量x的取值范围是：x≠-1
（2）列出y与x的几组对应值，请直接写出m的值，m=3．
| x | … | -5 | -4 | -3 | -2 | -$\frac{3}{2}$ | -$\frac{1}{2}$ | 0 | 1 | 2 | m | 4 | 5 | … |
| y | … | $\frac{5}{4}$ | $\frac{4}{3}$ | $\frac{3}{2}$ | 2 | 3 | -1 | 0 | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{3}{4}$ | $\frac{4}{5}$ | $\frac{5}{6}$ | … |
（4）结合函数的图象，写出函数y=$\frac{x}{x+1}$的一条性质．
如图，已知AB∥CF，DE∥CF，DE与BC交于点P，若∠ABC=70°，∠CDE=130°．