题目内容
1.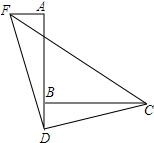 如图,已知∠ABC=90°,D是AB延长线上的点,AD=BC,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,求证:FD⊥CD.
如图,已知∠ABC=90°,D是AB延长线上的点,AD=BC,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,求证:FD⊥CD.
分析 利用SAS证明△AFD和△BDC全等即可解决问题.
解答 证明:∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
$\left\{\begin{array}{l}{AD=BC}\\{∠FAD=∠DBC}\\{AF=BD}\end{array}\right.$,
∴△FAD≌△DBC(SAS);
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴∠FDC=90°,
∴DF⊥CD.
点评 此题考查了全等三角形的判定与性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列实数中,比-7小的数为( )
| A. | 1 | B. | 0 | C. | -6 | D. | -8 |
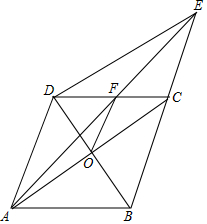 已知:如图,?ABCD中,对角线AC,BD相交于点O,延长BC至E,使CE=BC,连接AE交CD于点F.
已知:如图,?ABCD中,对角线AC,BD相交于点O,延长BC至E,使CE=BC,连接AE交CD于点F.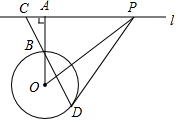 如图,直线l与⊙O相离,过点O作OA⊥l,垂足为A,OA交⊙O于点B,点C在直线l上,连接CB并延长交⊙O于点D,在直线l上另取一点P,使∠PCD=∠PDC.
如图,直线l与⊙O相离,过点O作OA⊥l,垂足为A,OA交⊙O于点B,点C在直线l上,连接CB并延长交⊙O于点D,在直线l上另取一点P,使∠PCD=∠PDC.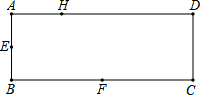 如图,矩形ABCD的长和宽分别为3和1,点E、F分别是AB、BC边的中点,点H在矩形ABCD边上,则使△EFH为直角三角形的点H的个数为( )
如图,矩形ABCD的长和宽分别为3和1,点E、F分别是AB、BC边的中点,点H在矩形ABCD边上,则使△EFH为直角三角形的点H的个数为( ) 如图,抛物线经过点A(-1,0)和B(0,2$\sqrt{2}$),对称轴为x=$\frac{5}{4}$.
如图,抛物线经过点A(-1,0)和B(0,2$\sqrt{2}$),对称轴为x=$\frac{5}{4}$. 如图使用五个相同的立方体搭成的几何体,从正面看的图形是( )
如图使用五个相同的立方体搭成的几何体,从正面看的图形是( )


